И реакций опор балок методом коэффициентов влияния
При формировании универсального уравнения упругой линии балки на шарнирных опорах возникает необходимость в определении угла поворота ее концевого опорного сечения в начале координат, то есть начального параметра j 0. Для этого приходится составлять и решать соответствующее уравнение, получаемое из граничного условия при z = ℓ (см. п. 3). Данную задачу можно упростить, если воспользоваться расчетной формулой для угла поворота опорного сечения (см. п. 5.6) [5].
где ℓ – длина пролета балки с шарнирными опорами по концам; Mj, Pj, ∆qj, ∆qj′ – параметры нагрузки в сечении j (см. рис. 5.3); αM, αP, α∆q, α∆q′ – соответствующие коэффициенты влияния, вычисляемые по формулам:
где ζ – безразмерная координата сечения j, в котором приложена нагрузка (Мj, Pj) или имеется скачок в интенсивности нагрузки (∆qj) и ее производных (∆q′j,…). Например, по рис. 5.3 имеем:
Значения коэффициентов влияния приведены в таблицах приложения к работе [6] (см. п. 5.6). Суммирование в формуле (Д.1) ведется по всем точкам j оси балки, в которых имеются особенности в нагрузке. Правила знаков для параметров нагрузки при вычислениях по формуле (Д.1) сохраняются те же, что при составлении универсального уравнения упругой линии балки. Остается в силе и замечание, касающееся использования левой системы координат с началом на правом конце балки. Применение формулы (Д.1) рассмотрим на примерах. Пример Д.1. Определить углы поворота опорных сечений балки (рис. Д.1).
Рисунок Д.1 – Расчетная схема к примеру Д.1
Решение: поместив начало координат в опорное сечение А, по формулам (Д.2) имеем:
Эти значения, не вычисляя, можно взять из таблиц [6] (см. п. 5.6). По формуле (Д.1) находим:
Сечение А повернулось по ходу часовой стрелки. Поместив начало координат в сечение В (на рис. Д.1 система осей О1yz показана пунктиром), получим:
По формуле (Д.1)
Сечение А повернулось против хода часовой стрелки. Рассмотренный пример показывает, что для определения углов поворота опорных сечений нет необходимости определять реакции опор балки. Однако для составления универсального уравнения упругой линии предварительное определение реакций опор обязательно. Так же как и углы поворота сечений, они могут быть найдены методом коэффициентов влияния. Соответствующая расчетная формула имеет вид (см. п. 5.6) [5]:
где Q0,P – поперечная сила в начале координат от нагрузки на пролете (начальный параметр), равная реакции опоры; rP, r∆q, r∆q′ – безразмерные коэффициенты влияния:
Формулы (Д.1) – (Д.4) справедливы лишь для балок с шарнирными опорами по концам. При начале координат в опорном сечении А (рис. Д.1) имеем:
По рисунку Д.1 и формуле (Д.3) находим:
При начале координат в сечении В:
Реакция YB направлена вниз. Проверка:
Универсальное уравнение упругой линии для балки (см. рис. Д.1):
Для проверки уравнения вычислим прогиб при z = ℓ (y(ℓ) = 0):
Возможность проверки составленного уравнения упругой линии балки является достоинством предложенного алгоритма его формирования. Формулу (Д.1) можно применять и в случае балки с консолями, но для этого необходимо предварительно нагрузку, приложенную на консоли, методами статики привести к опорному сечению балки. Пример Д.2. Определить углы поворота опорных сечений и перемещения концевых сечений двухконсольной балки (рис. Д.2). Решение: заданную на консолях нагрузку приводим к опорным сечениям балки, а сами консоли отбрасываем. В результате получаем расчетную схему (рис. Д.2, б).
Рисунок Д.2 – Расчетные схемы к примеру Д.2
При начале координат в сечении А имеем:
По формуле (Д.1) и рисунку Д.2 находим:
Сечение А повернулось против хода часовой стрелки. При начале координат в сечении В имеем:
Тогда
Сечение В повернулось по ходу часовой стрелки. Определим реакции опор по формуле (Д.3):
При этом отсчет координат z при вычислении YA ведем слева направо от опоры А, а при вычислении YВ – справа налево от опоры В. Проверка:
Реакции опор показаны на рис. Д.2, а. При известных углах поворота сечений А и В можно определить перемещения левого и правого концевых сечений балки, рассмотрев деформации консолей отдельно (рис. Д.3).
Рисунок Д.3 – Схемы к определению перемещений
|

 , (Д.1)
, (Д.1)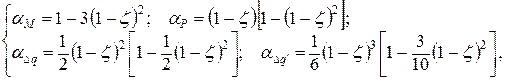 (Д.2)
(Д.2)





 (Д.3)
(Д.3) (Д.4)
(Д.4)

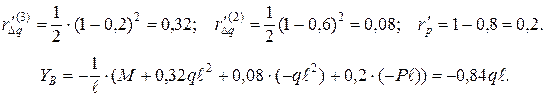
 .
.













