Ступенчато-переменного сечения
В связи с широким внедрением в расчетную практику ЭВМ наблюдается тенденция к уточнению расчетных схем сложных инженерных конструкций. Благодаря этому удается повысить надежность объекта расчета и сделать его более экономичным. Вместе с тем имеет место увеличение объема и усложнение структуры исходной информации, подготовка которой может составлять значительную часть общего времени решения задачи. Поэтому при разработке или выборе методики расчета конструкции последнее обстоятельство должно учитываться. Кроме того, для решения некоторых задач может оказаться нерациональным использование универсальных ЭВМ вследствие высокой стоимости машинного времени, значительных затрат времени на программирование, ввод исходных данных и др. В связи с этим во многих случаях расчет конструкции целесообразно проводить на программируемых микрокалькуляторах благодаря их доступности и простоте в обращении. Предложенные в настоящем пособии алгоритмы расчета балок ступенчато-переменной жесткости достаточно просто реализуются как на персональных ЭВМ, так и на программируемых микрокалькуляторах. Исходная информация представляется в удобной табличной форме. Никаких дополнительных построений, кроме чертежа расчетной схемы, для расчета заданной системы не требуется. Расчет рекомендуется проводить в матричной форме, что имеет заметное преимущество в сравнении с обычной методикой и при “ручном” счете, так как порядок используемых матриц перехода невелик (n = 4), а из всех возможных операций с матрицами используется только одна – перемножение квадратной матрицы (верхней треугольной) на матрицу-столбец (вектор), что легко осуществимо на микрокалькуляторах. Поскольку валы и балки ступенчато-переменного сечения являются весьма распространенными элементами конструкций, предлагаемая методика их расчета может быть полезной как студентам машиностроительных и строительных специальностей, так и инженерам-расчетчикам. Ж.1 Зависимости между концевыми параметрами бруса ступенчато-переменного сечения
Рассмотрим брус ступенчато-переменного поперечного сечения, находящийся в равновесии под действием произвольной статической нагрузки и внутренних силовых факторов в концевых сечениях, приложенных со стороны смежных элементов конструкции (рис. Ж.1).
Рисунок Ж.1 – Схема нагружения бруса
Отнесем брус к системе осей координат Указанные на рис. Ж.1 направления нагрузок, внутренних силовых факторов и углов поворотов сечений, так же как и в случае бруса постоянного сечения, считаем положительными [15]. Прогибы считаем положительными при перемещении сечений вдоль оси Введем в рассмотрение безразмерные параметры:
Зависимости между начальными (
где кi – погонная жесткость участка бруса:
Перепишем (Ж.1) в сжатой форме:
где
где нижние индексы Выражение (Ж.4) справедливо для каждого участка бруса ступенчато-переменного сечения, в том числе и для последнего участка, имеющего номер
Полагая в (Ж.4) последовательно
где
Выражение (Ж.6) с учетом (Ж.7) и (Ж.8) решает поставленную задачу, то есть устанавливает зависимости между концевыми параметрами бруса ступенчато-переменного сечения при произвольной поперечной статической нагрузке. Причем матрица
где
Если для всех ступеней
где Сопоставление матрицы (Ж.9) с соответствующей матрицей бруса постоянной жесткости показывает, что в последнем случае имеем:
Формулы (Ж.10) дают возможность вычислить компоненты матрицы непосредственно, не прибегая к перемножению матриц перехода участков бруса по формуле (Ж.7). Вектор
где После вычисления компонент вектора
где
Формула (Ж.15) позволяет определить угол поворота опорного сечения балки ступенчато-переменного сечения на шарнирных жестких опорах по концам непосредственно по данным чертежа расчетной схемы, не прибегая к дополнительной идеализации заданной системы и не делая каких-либо графических построений. Если учесть, что для этой балки на шарнирных опорах поперечная сила в начале координат от действия нагрузки на пролете, то есть
формулу (Ж.15) можно представить в виде:
В выражении (Ж.17) величину Пример применения формулы (Ж.15) к определению прогибов ступенчатого вала рассмотрен в п. Ж.3.
Ж.2 Алгоритм определения перемещений в статически определимых балках на шарнирных жестких опорах
На основании изложенного в п. Ж.1 для балок с шарнирными жесткими опорами по концам расчет граничных параметров участков и перемещений в пределах каждого участка целесообразно проводить в следующей последовательности: 1. Подготовить исходную информацию о конструктивных параметрах расчетного объекта. Необходимые для формирования матриц перехода данные удобно свести в таблицу (табл. Ж.1). Таблица Ж.1 – Параметры для расчета балки ступенчато-
2. Сформировать матрицы перехода участков балки:
3. По формулам (Ж.10) вычислить значения безразмерных коэффициентов 4. Сформировать матрицу перехода
5. Вычислить компоненты векторов 6. Последовательно выполнить вычисления по рекуррентным зависимостям (Ж.8) и сформировать матрицу-столбец 7. Вычислить угол поворота 8. Вычислить 9. Сформировать матрицу-столбец начальных параметров 10. Определить геометрические и силовые параметры балки в сечениях на границах участков и в правом концевом сечении, пользуясь зависимостью (Ж.4). 11. Проверить полученные в правом концевом сечении значения параметров по (Ж.6). 12. Вычислить перемещения в характерных сечениях каждого участка. Поскольку каждый участок имеет постоянную жесткость, а граничные параметры уже найдены, эта задача легко решается известными методами [15]. Для балки с шарнирными опорами, имеющей консоль, предложенный алгоритм также применим, если нагрузку, приложенную к консоли, предварительно методами статики привести к крайней опоре и отнести получаемые в результате приведения силовые факторы (силу и момент) к нагрузке пролета.
|



 с началом в левом концевом сечении.
с началом в левом концевом сечении. , то есть вверх (на рис. Ж.1 перемещения
, то есть вверх (на рис. Ж.1 перемещения  и
и  не показаны). Участки бруса, имеющие постоянное поперечное сечение, нумеруем слева направо, начиная с I. Номер участка совпадает с номером правого концевого сечения этого участка.
не показаны). Участки бруса, имеющие постоянное поперечное сечение, нумеруем слева направо, начиная с I. Номер участка совпадает с номером правого концевого сечения этого участка. - соответственно длина ступени I и расстояния ее середины
- соответственно длина ступени I и расстояния ее середины  от левого и правого концов бруса, выраженные в долях его длины
от левого и правого концов бруса, выраженные в долях его длины  .
. ) и конечными (
) и конечными (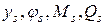 ) параметрами постоянного сечения в случае произвольной статической нагрузки получены в [20]. Воспользуемся ими для нахождения аналогичных зависимостей между концевыми параметрами бруса ступенчато-переменной жесткости (см. рис. Ж.1).
) параметрами постоянного сечения в случае произвольной статической нагрузки получены в [20]. Воспользуемся ими для нахождения аналогичных зависимостей между концевыми параметрами бруса ступенчато-переменной жесткости (см. рис. Ж.1).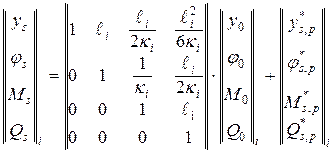 , (Ж.1)
, (Ж.1) ; (Ж.2)
; (Ж.2) – модуль упругости материала;
– модуль упругости материала;  – осевой момент инерции поперечного сечения.
– осевой момент инерции поперечного сечения. , (Ж.3)
, (Ж.3) – соответственно матрицы-столбцы (векторы) начальных и конечных параметров участка
– соответственно матрицы-столбцы (векторы) начальных и конечных параметров участка  ;
;  – матрица перехода этого участка;
– матрица перехода этого участка;  – матрица-столбец участка
– матрица-столбец участка  проводится по уравнениям метода начальных параметров, составляемым для этого участка. При этом начало системы осей координат помещается в начало участка. Поскольку номер участка i совпадает с номером правого концевого сечения этого участка, выражение (Ж.3) можно записать в следующем виде:
проводится по уравнениям метода начальных параметров, составляемым для этого участка. При этом начало системы осей координат помещается в начало участка. Поскольку номер участка i совпадает с номером правого концевого сечения этого участка, выражение (Ж.3) можно записать в следующем виде: , (Ж.4)
, (Ж.4) указывают номер сечения, в котором определяются граничные параметры участка, а верхние индексы – номер участка бруса.
указывают номер сечения, в котором определяются граничные параметры участка, а верхние индексы – номер участка бруса. , для которого согласно (Ж.4) имеем:
, для которого согласно (Ж.4) имеем: . (Ж.5)
. (Ж.5) и поочередно подставляя получаемые выражения в (Ж.5), получим:
и поочередно подставляя получаемые выражения в (Ж.5), получим: , (Ж.6)
, (Ж.6) – матрица перехода элемента
– матрица перехода элемента  ступенчато-переменной жесткости (см. рис. Ж.1):
ступенчато-переменной жесткости (см. рис. Ж.1): ; (Ж.7)
; (Ж.7)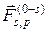 – вектор, учитывающий влияние нагрузки, приложенной к брусу
– вектор, учитывающий влияние нагрузки, приложенной к брусу  . Для его определения получаем рекуррентные выражения:
. Для его определения получаем рекуррентные выражения: (Ж.8)
(Ж.8)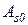 , как показывает анализ ее структуры по (Ж.7), может быть представлена в виде:
, как показывает анализ ее структуры по (Ж.7), может быть представлена в виде: , (Ж.9)
, (Ж.9) – безразмерные коэффициенты податливостей бруса
– безразмерные коэффициенты податливостей бруса  :
: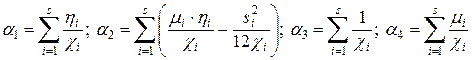 ; (Ж.10)
; (Ж.10) – безразмерные погонные жесткости его ступеней:
– безразмерные погонные жесткости его ступеней: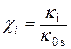 ; (Ж.11)
; (Ж.11) – средняя погонная жесткость бруса
– средняя погонная жесткость бруса  .
. то
то , (Ж.12)
, (Ж.12) – среднее значение осевого момента инерции сечения бруса
– среднее значение осевого момента инерции сечения бруса 
 , входящий в (Ж.6), вычисляется рекуррентно по формуле (Ж.8). Причем вектор
, входящий в (Ж.6), вычисляется рекуррентно по формуле (Ж.8). Причем вектор  , с которого начинается расчет, имеет вид:
, с которого начинается расчет, имеет вид: , (Ж.13)
, (Ж.13)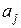 – расстояние от начала участка длиной
– расстояние от начала участка длиной  до точки
до точки  , в которой имеются скачки в нагрузке
, в которой имеются скачки в нагрузке  . Суммирование в (Ж.13) ведется по индексу
. Суммирование в (Ж.13) ведется по индексу  , то есть учитывается влияние всей нагрузки на данном участке. Правила знаков для параметров нагрузки те же, что при составлении универсального уравнения упругой линии. Аналогичные выражения имеют место для векторов
, то есть учитывается влияние всей нагрузки на данном участке. Правила знаков для параметров нагрузки те же, что при составлении универсального уравнения упругой линии. Аналогичные выражения имеют место для векторов  и т.д. Если нагрузка на участке бруса отсутствует, компоненты соответствующего вектора будут нулевыми.
и т.д. Если нагрузка на участке бруса отсутствует, компоненты соответствующего вектора будут нулевыми. по (Ж.8) нетрудно найти значения геометрических и силовых параметров в правом концевом сечении бруса по выражению (Ж.6). Следствием зависимостей между концевыми параметрами бруса ступенчато-переменного сечения в (Ж.6) является формула для вычисления угла поворота поперечного сечения бруса в начале координат:
по (Ж.8) нетрудно найти значения геометрических и силовых параметров в правом концевом сечении бруса по выражению (Ж.6). Следствием зависимостей между концевыми параметрами бруса ступенчато-переменного сечения в (Ж.6) является формула для вычисления угла поворота поперечного сечения бруса в начале координат: , (Ж.14)
, (Ж.14) . (Ж.15)
. (Ж.15) , равная реакции опоры, связана с
, равная реакции опоры, связана с  зависимостью
зависимостью , (Ж.16)
, (Ж.16) . (Ж.17)
. (Ж.17)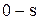 , а для нахождения значения
, а для нахождения значения  , являющегося первой компонентой вектора
, являющегося первой компонентой вектора  , м
, м

 , м
, м

 , м
, м


 , Нм
, Нм
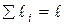

 . (Ж.18)
. (Ж.18)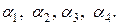
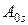 согласно (Ж.9), приняв
согласно (Ж.9), приняв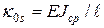 . (Ж.19)
. (Ж.19)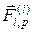 по (Ж.13) и представить последние в виде матриц-столбов.
по (Ж.13) и представить последние в виде матриц-столбов. левого опорного сечения балки по формуле (Ж.15).
левого опорного сечения балки по формуле (Ж.15). по формуле (Ж.16) и проверить полученный результат по уравнению равновесия статики для балки
по формуле (Ж.16) и проверить полученный результат по уравнению равновесия статики для балки 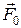 .
.


