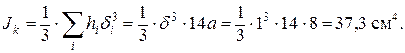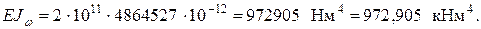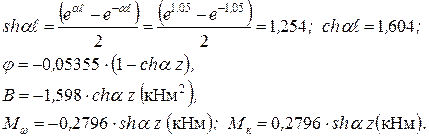Пример выполнения задания
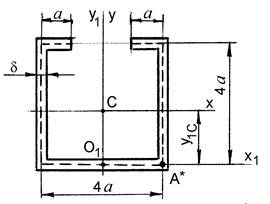
Пример решения задачи № 1 Дан тонкостенный стальной стержнь длиной ℓ;, имеющий форму поперечного сечения (рис. 10.7) и нагруженный продольной растягивающей силой Р, приложенной к незакрепленному концевому сечению в т. А. (Записать текст задания по п. 10.1). Данные: Р = 90 кН, ℓ; = 6 м, a = 8 см, d = 1см.
Рисунок 10.7 – Схема заданного поперечного сечения стержня
Закрепленное концевое сечение стержня жестко заделано. Решение: 1. Определяем положение центра тяжести сечения. Данное сечение имеет ось симметрии (ось у). Поэтому центр тяжести сечения расположен на этой оси. Его координата относительно оси х (рис. 10.7):
Для проверки вычислений определим статический момент сечения относительно оси х, который должен быть равен нулю:
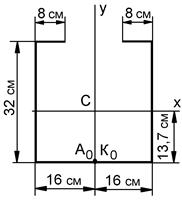
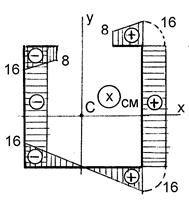
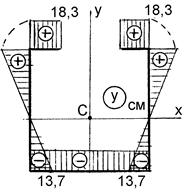
Незначительное отклонение от нуля связано с округлением значения у 1 с . Вычерчиваем контур сечения в масштабе (рис. 10.8, а) и строим эпюры линейных координат х, у точек контура (рис. 10.8, б, в).
а б в
Рисунок 10.8 – Построение эпюр линейных координат
По формулам (10.26), применив способ А.К. Верещагина, находим главные центральные моменты инерции сечения:
2. Определяем положение центра изгиба сечения. Согласно формулам (10.22), необходимо найти секториальные центробежные моменты инерции сечения с использованием произвольно выбираемых вспомогательного полюса А0 и начальной Выбираем точку А0 на оси симметрии у (см. рис. 10.8, а), а точку К0 совместим с точкой А0. Строим эпюру вспомогательных секториальных координат (см. пример в п. 10.2.4). Эпюра w0 приведена на рис. 10.9, а.
а б
Рисунок 10.9 – Построение эпюр w 0 и w
По формулам (10.25), применив способ А.К. Верещагина, находим значения Jw 0 У и Jw 0 Х , перемножив эпюру w 0 соответственно с эпюрами х и у:
По формулам (10.22) находим положение главного полюса А (центр изгиба):
Откладываем координату ау от вспомогательного полюса А0 и строим эпюру главных секториальных координат (см. рис. 10.9, б). Эта эпюра характеризует депланацию сечения (см. (10.12)). В данном случае главная нулевая секториальная точка К совпадает с точкой К0. Перемножая эпюру w саму на себя по способу А.К. Верещагина, согласно (10.25) находим секториальный момент инерции сечения:
3. Определяем внутренние силовые факторы в поперечных сечениях стержня. Координаты точки приложения силы: хр = 16 см, ур = -13,7см, wр = -284,8 см2. Внутренние силовые факторы в поперечном сечении, примыкающем к свободному концевому сечению: нормальная сила: N = Р = 99 кН; изгибающие:
бимомент: крутящий момент: Mz = Mк + M w = 0. Внутренние усилия N, My, Mx по длине стержня не изменяются, то есть их эпюры имеют форму прямоугольника. Бимомент В, крутящий момент свободного кручения Мк, изгибно-крутящий момент Мw по длине стержня изменяются. Для их определения воспользуемся уравнениями (10.41). Поместим начало координат в центр тяжести заделанного сечения стержня (на рис. 10.7 ось z проходит через т. С и направлена к наблюдателю). По уравнениям метода начальных параметров (10.41) имеем:
Входящие в это уравнение начальные параметры
Р wр = В 0 chaℓ;,
откуда Следовательно, согласно уравнениям (10.41), имеем:
Значение геометрической характеристики крутильной жесткости Jк, входящей в уравнение для углов закручивания j, найдем по формуле (10.3):
Тогда Изгибно-крутильную характеристику жесткости a определим по (10.28):
где Учитывая найденные значения, получим:
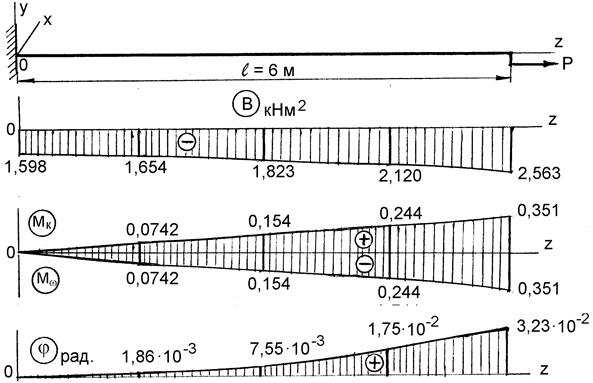
Вычислим значения j, В, Мw, Мк в ряде сечений стержня и построим соответствующие эпюры (табл. 10.3, рис. 10.10).
Таблица 10.3 – Значения j, В, Мw, Мк для построения эпюр
Рисунок 10.10 – Схема нагружения стержня и эпюры j, Мw, Мк
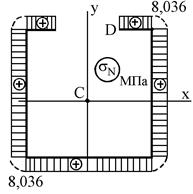
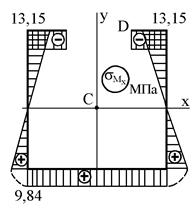
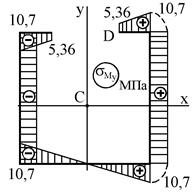
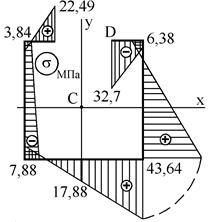
4. Строим эпюру распределения нормальных напряжений в сечении стержня, прилегающем к его свободному торцу. Для этого определим законы распределения напряжений от действия внутренних силовых факторов в отдельности:
Пользуясь этими зависимостями, строим эпюры распределения напряжений от действия каждого внутреннего силового фактора
а б в
г д
Рисунок 10.11 – Эпюры нормальных напряжений
В результате суммирования напряжений, найденных от каждого силового фактора, получаем результирующие напряжения в характерных точках и строим окончательную эпюру нормальных напряжений (см. рис. 10.11, д).
|


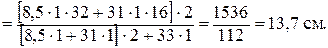
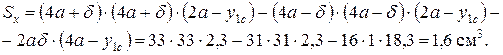


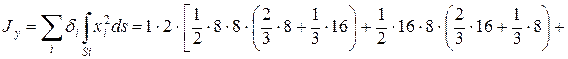
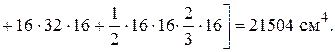


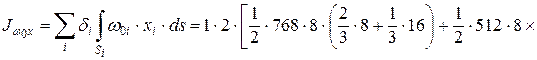
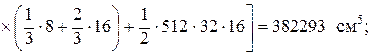
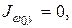 так как перемножение кососимметричной эпюры w 0 с симметричной эпюрой y дает нуль.
так как перемножение кососимметричной эпюры w 0 с симметричной эпюрой y дает нуль.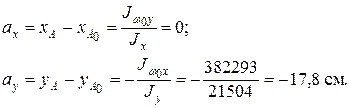
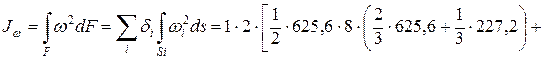


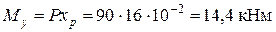 ;
;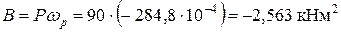 ;
;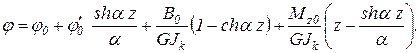
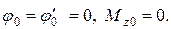 Остается определить бимомент В 0 в заданном сечении. Из граничного условия для свободного торца: х = ℓ;, В = Р wр. Пользуясь третьим уравнением (10.41), получаем:
Остается определить бимомент В 0 в заданном сечении. Из граничного условия для свободного торца: х = ℓ;, В = Р wр. Пользуясь третьим уравнением (10.41), получаем: = Р wр / chaℓ;.
= Р wр / chaℓ;.