Суммарный крутящий момент в текущем сечении
Мz = Мк + Мw (10.8) может быть найден по уравнениям равновесия статики, если задача статически определима. При кручении нормальная сила N и изгибающие моменты Мх, Му в поперечных сечениях стержня отсутствуют:
где х, у – декартовы координаты точки в главных центральных осях сечения. Последние зависимости показывают, что секториальные нормальные напряжения sw являются самоуравновешенными. 10.2.3 Основные гипотезы и расчетные зависимости для определения напряжений при стесненном кручении
В основе теории тонкостенных стержней открытого профиля лежат две гипотезы: 1. Контур поперечного сечения стержня не деформируется в своей плоскости (гипотеза жесткого контура). 2. В срединной поверхности стержня отсутствуют угловые деформации. Из первой гипотезы следует, что контур поперечного сечения при деформировании стержня поворачивается как жесткое целое вокруг некоторой точки А, называемой центром кручения. Однако при этом точки контура перемещаются в осевом направлении (депланация). Обозначим составляющие полного перемещения любой точки М, лежащей в срединной поверхности стержня, соответственно в окружном и осевом направлениях через v и w. Пользуясь рисунком 10.4, а, находим:
где j – угол поворота сечения; r – расстояние от т. А до касательной к контуру сечения в т. М. Пунктиром на рисунке 10.4, а обозначено начальное положение контура. Согласно известным из теории упругости геометрическим уравнениям Коши, угловая деформация gsz в точках срединной поверхности стержня выражается через перемещения v и w:
где s – дуговая координата точки; z – осевая координата.
a б в
Рисунок 10.4 – Схемы к выводу геометрических соотношений для тонкостенного открытого профиля Отсюда согласно второй гипотезе имеем:
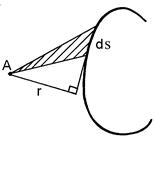
Учитывая (10.10) и интегрируя по s от некоторой начальной точки К до точки М, получаем (рис. 10.4, в):
где rds – удвоенная площадь элементарного сектора (рис. 10.4, б):
– секториальная площадь, или секториальная координата точки М. Начальную точку К выбирают так, чтобы в этой точке отсутствовало осевое перемещение (w 0 = 0). Секториальная координата w точки М равна удвоенной площади криволинейного треугольника, описываемого лучом, направленным из т. А (рис. 10.4, в). Будем считать ее положительной, если при взгляде со стороны положительного направления оси z поворот луча происходит против хода часовой стрелки. Допуская, что продольные волокна стержня не давят друг на друга, по закону Гука для одноосного напряженного состояния
где ez – продольная линейная деформация; по формуле Коши
С учетом (10.12)
Тогда Подставив (10.14) в (10.6), имеем:
где Jw – секториальный момент инерции сечения (см6):
Формула (10.14) с учетом (10.15) принимает вид:
Если функция угла закручивания j = j (z) найдена, то по выражению (10.15) легко определить бимомент В в любом сечении стержня. Чтобы воспользоваться формулой (10.17) для вычисления напряжений sw, предварительно следует найти секториальные координаты w точек сечения (построить эпюру w) и вычислить значение Jw по формуле (10.16). Секториальные касательные напряжения tw определяют по формуле
где Мw определяется по (10.7):
d – толщина стенки стержня;
Вывод формулы (10.18) аналогичен выводу известной из теории изгиба формулы Д.И. Журавского. Заметим, что по (10.18) определяются напряжения tw, действующие в продольном сечении стержня, проходящем через исследуемую точку поперечного сечения. Они положительны, если действуют в отрицательном направлении оси z (при обходе контура против хода часовой стрелки). В поперечном сечении их направления определяют по закону парности касательных напряжений.
10.2.4 Определение секториальных координат точек профиля и секториальных геометрических характеристик сечения
Центр кручения А и начальная точка К при определении секториальных координат w (см. рис. 10.4) должны выбираться так, чтобы соблюдались условия (10.9), из которых с учетом формулы (10.17) следует:
где S – секториальный статический момент сечения (см4); В литературе два последних интеграла часто называют секториально-линейными статическими моментами и обозначают соответственно Swy, Swx. Точка А, относительно которой Jwx, Jwy равны нулю, называется главным полюсом. Координаты главного полюса А в главных центральных осях поперечного сечения определяют по формулам:
где w 0 – секториальные координаты относительно произвольно выбранных полюса А0 и начальной точки К0; xА, yА – координаты главного полюса А (центра изгиба, центра кручения); Чтобы удовлетворить первому равенству (10.21), следует определить секториальную координату w / начальной точки К с использованием главного полюса А и произвольной начальной точки К0:
Секториальные координаты точек средней линии сечения, найденные с использованием точек А и К, называемые главными (истинными) секториальными координатами w, могут быть вычислены по формуле
где Вывод формул (10.22) – (10.24) приводится в учебниках [1 – 4]. Точки, в которых w = 0, называются нулевыми секториальными точками. Ближайшая из этих точек к центру кручения (главному полюсу А) считается главной нулевой секториальной точкой. Эта точка и принимается в качестве начальной точки К. Если сечение имеет ось симметрии, то центр кручения А, совпадающий с центром изгиба, находится на оси симметрии, а точка К находится на пересечении этой оси со средней линией сечения. У сечений в форме уголка или тавра центр кручения находится в точке пересечения средних линий элементов профиля. При нагружении стержня изгибающими силами кручение будет отсутствовать, если линии действия этих сил пересекают ось изгиба стержня (геометрическое место точек, совпадающих с центрами изгиба сечений). При вычислении секториальных геометрических характеристик сечения Для этого предварительно строят на контуре сечения эпюры секториальных координат, которые затем перемножают, учитывая, что в этом случае все эпюры линейные.
где di – толщина i -го участка профиля; ds – элемент длины контура. Главные центральные моменты инерции сечения, принимая во внимание тонкостенность профиля, также могут быть вычислены способом А.К. Верещагина:
Техника вычисления геометрических характеристик сечений тонкостенных стержней подробно рассмотрена в [2, 4, 5, 6]. Пример Для сечения в форме швеллера (рис. 10.5, а) вычислить необходимые геометрические характеристики [3]. Выбираем вспомогательные точки А0 (полюс) и К0 (начальная точка отсчета) на пересечении оси симметрии со средней линией стенки
а б в г д
Рисунок 10.5 – К определению геометрических характеристик швеллера
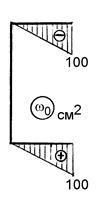
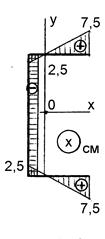
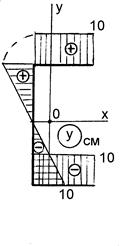
Так как поворот луча происходит против хода часовой стрелки, то эта координата положительна. Для точки М3 получаем: w 0(М3) = -100 см2. Эпюра секториальных координат w 0 приведена на рис. 10.5, в. Строим эпюры линейных координат точек контура (рис. 10.5, г, д). Перемножая эпюры w 0 и x, w 0 и y по правилу А.К. Верещагина, соответственно находим:
Первый интеграл равен нулю, так как эпюра x симметрична относительно оси Ох, а эпюра w 0 – кососимметричная. Перемножением эпюр х и у самих на себя вычисляем главные центральные моменты инерции сечения:
По формулам (10), (22) находим положение центра кручения:
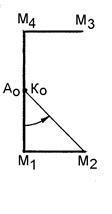
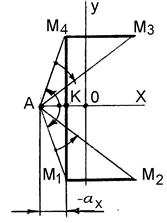
На рисунке 10.6, а показано положение центра кручения А (главный полюс, центр изгиба) и главной нулевой секториальной точки К. Кривыми стрелками на рис. 10.6, а показаны направления вращения луча, исходящего из т. А, при определении главных секториальных координат. Начальное положение луча – АК.
а б
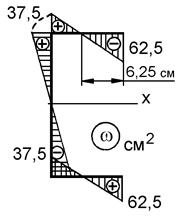
Рисунок 10.6 – Построение эпюры главных секториальных координат
Вычисляем значения w в характерных точках: wК = 0.
Эпюра главных секториальных координат (рис. 10.6, б) характеризует депланацию сечения. В данном случае положение главной нулевой секториальной точки К было известно. Поэтому вычисления по формуле (10.23) не потребовались. Перемножив эпюру саму на себя по правилу А.К. Верещагина, находим секториальный момент инерции сечения:
10.2.5 Дифференциальное уравнение стесненного кручения и его решение
Функция j (z) углов закручивания стержня является определяющей (см. п. 10.2.3), так как после ее нахождения нетрудно определить внутренние силовые факторы и напряжения в сечениях стержня. При выводе дифференциального уравнения для этой функции исходят из равенства (10.8), откуда в результате дифференцирования по z, с учетом зависимостей (10.1), (10.19) получаем:
где a – изгибно-крутильная характеристика жесткости стержня:
m – интенсивность внешней скручивающей нагрузки, которую считаем положительной, если при взгляде со стороны положительного направления оси z она направлена по ходу часовой стрелки:
Общее решение уравнения (10.27) имеет вид:
где j* – частное решение неоднородного уравнения (10.27), зависящее от вида функции нагрузки m (z). Постоянные С 1, С 2, С 3, С 4 определяют из граничных условий. Если на конце стержня имеется жесткая заделка, то в этом сечении j = 0, Последнее условие вытекает из (10.12) при w = 0. Если концевое сечение стержня ограничено от поворота, но депланация сво- j = 0, В = 0. (10.32) Второе условие обусловлено отсутствием нормальных напряжений sw (см. (10.6)). При нагружении стержня внешним скручивающим моментом М в незакрепленном (свободном) концевом сечении
Если же в незакрепленном сечении стержня приложена продольная сосредоточенная сила Р, то в этом сечении
где wр – главная секториальная координата точки приложения силы. Входящие в (10.30) гиперболические синус и косинус удобно вычислять с использованием микрокалькулятора:
Удовлетворяя граничным условиям стержня, получают систему алгебраических уравнений относительно искомых постоянных С 1, С 2, С 3, С 4. После решения этой системы уравнений по формулам:
определяют внутренние силовые факторы в сечениях стержня, а затем вычисляют напряжения sw, tw по (10.17), (10.18). При наличии нескольких участков стержня, то есть в случаях нагружения последнего в промежуточных сечениях, решение задачи усложняется. В этих случаях на практике часто пользуются методом начальных параметров.
|

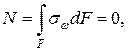
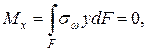
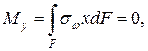 (10.9)
(10.9)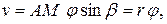 (10.10)
(10.10) (10.11)
(10.11)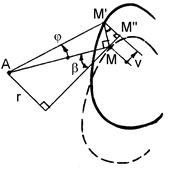

 .
.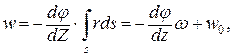 (10.12)
(10.12) (10.13)
(10.13) ,
,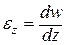 .
.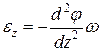 .
.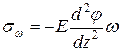 . (10.14)
. (10.14) , (10.15)
, (10.15)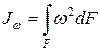 . (10.16)
. (10.16) . (10.17)
. (10.17)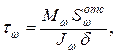 (10.18)
(10.18)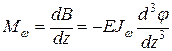 ; (10.19)
; (10.19)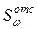 – секториальный статический момент отсеченной части площади сечения:
– секториальный статический момент отсеченной части площади сечения: . (10.20)
. (10.20)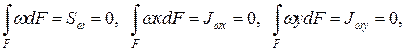 (10.21)
(10.21)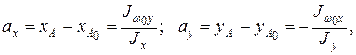 (10.22)
(10.22) – координаты вспомогательного полюса А0; аx, аy – координаты главного полюса А относительно произвольного полюса А0.
– координаты вспомогательного полюса А0; аx, аy – координаты главного полюса А относительно произвольного полюса А0. . (10.23)
. (10.23) (10.24)
(10.24)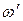 – секториальные координаты, получаемые с использованием точек А и К0.
– секториальные координаты, получаемые с использованием точек А и К0.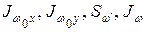 , входящих в формулы (10.16), (10.22), (10.23), если сечение состоит из прямолинейных элементов, применяют способ А.К. Верещагина.
, входящих в формулы (10.16), (10.22), (10.23), если сечение состоит из прямолинейных элементов, применяют способ А.К. Верещагина.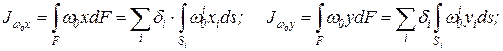
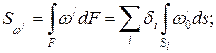
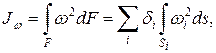 (10.25)
(10.25)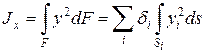 ;
;  . (10.26)
. (10.26)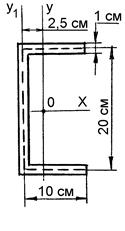
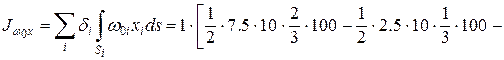
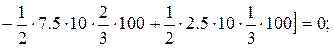
 см5.
см5.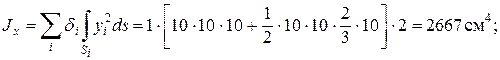



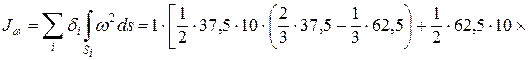

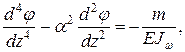 (10.27)
(10.27)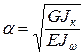 ; (10.28)
; (10.28) . (10.29)
. (10.29)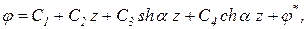 (10.30)
(10.30)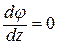 . (10.31)
. (10.31) (10.33)
(10.33)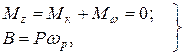 (10.34)
(10.34)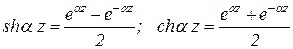 . (10.35)
. (10.35) (10.36)
(10.36)


