Для узкого прямоугольного сечения
где h – размер длинной стороны прямоугольника, а d – короткой (толщина). Если сечение состоит из нескольких прямоугольников и прокатных профилей, применяют формулу
где h 1, di – размеры отдельных прямоугольников профиля, hn – коэффициент формы профиля (для двутавра h = 2, швеллера - h = 1,12, уголка и листа - h = 1). Например, для швеллера
где hc, dc – размеры стенки; hn, dn – полки. Если сечение имеет криволинейную форму, то
где s – длина контура по средней линии профиля. 10.2.2 Напряжения и внутренние силовые факторы при стесненном кручении
Секториальные нормальные и касательные напряжения обозначают соответственно sw, tw (w – секториальная координата точки профиля, в которой определены данные напряжения). Кроме этих напряжений в сечении действуют касательные напряжения свободного кручения tк, определяемые по формулам п. 10.2.1. По толщине профиля напряжения tк, и tw распределены по различным законам. Напряжениям tк соответствует треугольная эпюра распределения. В точках средней линии контура tк = 0, а в крайних точках по толщине профиля tк = t mах, где t mах определяется по (10.1). Секториальные касательные напряжения tw по толщине профиля распределяются равномерно. Трем видам напряжений, возникающим при стесненном кручении стержня открытого профиля, соответствуют три внутренних силовых фактора. Нормальные напряжения sw приводятся к бимоменту В:
где F – площадь сечения; w – секториальная координата точки. Касательные напряжения tw приводятся к изгибно-крутящему моменту Мw:
где z – координата поперечного сечения стержня. Касательные напряжения tк приводятся к крутящему моменту свободного кручения Мк, а наибольшие их значения определя-
|


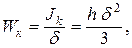 (10.2)
(10.2) (10.3)
(10.3)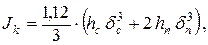 (10.4)
(10.4)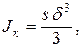
 , (10.5)
, (10.5)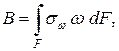 (10.6)
(10.6) (10.7)
(10.7)


