Ступенчато-переменного сечения. Для балки (рис. Ж.3) требуется определить угол поворота концевого сечения.
Для балки (рис. Ж.3) требуется определить угол поворота концевого сечения.
Рисунок Ж.3 – Расчетная схема консольной балки Решение: составляем таблицу исходных данных (табл. Ж.3). Таблица Ж.3 – Данные для расчета консольной балки
Проверяем результаты заполнения таблицы, используя зави-симости:
По формулам (Ж.10) находим:
Формируем матрицу
Формируем матрицы-столбцы
Используя рекуррентные зависимости (Ж.8), находим:
Вектор начальных параметров:
Согласно (Ж.6), имеем:
Заметим, что сечение 3, в котором определены концевые параметры, являющиеся компонентами вектора Для сравнения определим прогиб и угол поворота концевого сечения балки постоянного сечения, имеющей
Ступенчатая балка в данном случае является более жесткой, чем фиктивная балка постоянного сечения при В рассмотренном примере матрицы перехода участков не использовались, так как не требовалось определять граничные параметры участков балки, и, кроме того, отсутствовала нагрузка на участках, расположенных левее правого концевого участка. Поэтому В других случаях использование матриц перехода участков становится обязательным. Рекомендуемая последовательность расчета изложена в п. Ж.4. При необходимости пользования левой системой координат, то есть при начале координат на правом конце участка и направлении оси Подробнее этот вопрос рассмотрен в [15]. Приведенные в пп. Ж.3 и Ж.5 примеры расчетов балок ступенчато-переменного сечения показаны в общем виде, то есть без использования численных значений параметров расчетного объекта и действующей нагрузки (в буквенных обозначениях), имеют в основном иллюстративное значение, способствуя быстрому усвоению предложенной методики расчета. С этой же целью подробно показаны необходимые действия с матрицами и приведены все промежуточные записи и числовые подстановки в расчетные формулы. При выполнении расчета в численной форме, что в большинстве случаев расчетной практики и делается, организация вычислений сохраняется в соответствии с изложенным в пп. Ж.2 и Ж.4. При этом в таблицу записываются численные значения параметров заданной системы с указанием их единиц измерения (см. табл. Ж.1). Также численно представляются компоненты матриц перехода и матриц-столбцов. В случае использования в расчете программируемого микрокалькулятора следует иметь в виду, что вычисление безразмерных коэффициентов податливостей При пользовании персональными ЭВМ могут быть предложены различные варианты программ, реализующие разработанные в настоящем пособии алгоритмы. Расчет элементов конструкций ступенчато-переменного сечения может выполняться различными методами. Целесообразность выбора того или иного из них определяется как конструктивными особенностями расчетного объекта, так и действующей нагрузкой. В [21] рассмотрена методика расчета на изгиб ступенчатого вала по способу замены его эквивалентной балкой постоянного сечения, имеющей те же перемещения, что и заданный ступенчатый вал. К недостаткам такого подхода можно отнести: – необходимость дополнительной схематизации конструкции, что требует определенных затрат времени; – значительное усложнение нагрузки на получаемую фиктивную балку в сравнении с заданной исходной схемой за счет приложения дополнительных нагрузок на границах ступеней вала; – неизбежность увеличения погрешностей в результатах расчета за счет округлений значений дополнительных нагрузок и большого их числа. Этих недостатков можно избежать, если воспользоваться методом начальных параметров в матричной форме [21]. Однако изложенный в [21] алгоритм имеет другие недостатки: 1) число участков балки может значительно превышать число ее ступеней, так как границами участков являются не только границы ступеней, но и точки приложения внешних сил, что приводит к увеличению затрат времени на матричные операции и поэтому ставит под сомнение целесообразность применения микрокалькуляторов; 2) распределенная нагрузка в пределах каждого участка имеет постоянную интенсивность, более сложная нагрузка из рассмотрения исключена; 3) неизвестные начальные параметры определяются из граничных условий традиционным способом, что при матричной форме расчета нерационально; 4) отсутствуют контрольные операции, позволяющие проверить достоверность результатов расчета. На основании ранее изложенного можно считать, что предложенные в настоящем пособии расчетные алгоритмы, свободные от перечисленных недостатков, могут успешно применяться в инженерной практике даже при "ручном" счете, с использованием микрокалькуляторов. ПРИЛОЖЕНИЕ И (справочное)
|















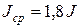
 .
.



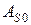 , пользуясь формой (Ж.9):
, пользуясь формой (Ж.9): .
.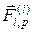 по (Ж.13):
по (Ж.13): .
. .
. .
.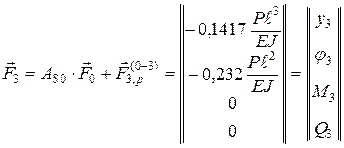 .
. , находится правее точки приложения силы
, находится правее точки приложения силы 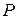 . Поэтому
. Поэтому  .
. :
: .
.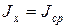 .
. матрицы перехода не потребо-
матрицы перехода не потребо- влево, а оси
влево, а оси  – вверх, следует иметь в виду, что при составлении вектора
– вверх, следует иметь в виду, что при составлении вектора  , направленные против хода часовой стрелки, учитываются со знаком (+), а углы поворота сечений положительны, если сечения поворачиваются по ходу часовой
, направленные против хода часовой стрелки, учитываются со знаком (+), а углы поворота сечений положительны, если сечения поворачиваются по ходу часовой 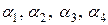 целесообразно осуществлять по предварительно составленным программам, пользуясь данными таблицы Ж.1 и не прибегая к промежуточным записям. Так же легко по составленной программе может быть организовано перемножение матрицы перехода на матрицу-столбец (вектор) путем последовательного умножения ее строк на этот вектор.
целесообразно осуществлять по предварительно составленным программам, пользуясь данными таблицы Ж.1 и не прибегая к промежуточным записям. Так же легко по составленной программе может быть организовано перемножение матрицы перехода на матрицу-столбец (вектор) путем последовательного умножения ее строк на этот вектор.


