Характеристик плоских сечений сложной формы
Предположим, что задано конкретное сечение (см. рис. И.3). Чертеж сечения должен быть выполнен строго в масштабе. Отнесем заданное сечение к прямоугольной системе координат Оxy. Причем ось Оx должна быть параллельна основаниям элементарных фигур (см. рис. И.1), на которые предварительно разбивается сечение. Указываем на чертеже центры тяжести составляющих площадей и их координаты x ( i ) и y ( i ), измеряемые в cантиметрах. Проводим оси xi и yi через центры тяжести составляющих площадей, которые должны быть параллельны осям Ох и Oy. Все необходимые размеры (в см) могут быть получены непосредственным измерением и указаны на чертеже. Образуем векторы (одномерные массивы) горизонтальных и вертикальных размеров элементарных фигур (для круга и частей круга указываем радиус):
Обозначения размеров соответствуют рисунку И.1 (измеряются в сантиметрах). Образуем векторы:
коэффициентов формы (см. рис. И.1 и И.3):
знаков площадей (см. рис. И.3 и И.4):
знаков центробежного момента инерции (см. рис. И.2 и И.3):
Образуем векторы координат центров тяжести элементарных площадей (см. рис. И.3):
Построенные семь одномерных массивов представляют собой исходную информацию, задаваемую ЭВМ, которая, получив входные данные, должна сформировать одномерные массивы площадей элементарных фигур и моментов инерции этих фигур относительно их центральных осей (всего четыре массива). Затем вычисляется площадь сечения, статические моменты сечения относительно осей Оx, Оу, а также координаты центра тяжести всего сечения:
Вслед за этим вычисляются осевые и центробежный моменты инерции сечения относительно центральных осей Сx и Сy, соответственно параллельных осям Оx и Оу:
Если Если
В качестве выходных данных принимаем: F; xc; yc; α;; Блок-схема алгоритма вычисления главных центральных моментов инерции сечения приведена на рис. И.5.
Рисунок И.5а – Схема алгоритма определения геометрических характеристик сечения (начало)
характеристик сечения (окончание) Подпрограмма FORM соответствует алгоритму формирования массивов площадей и моментов инерции из соответствующих характеристик элементарных фигур (рис. И.6).
Рисунок И.6 – Схема алгоритма формирования массивов FM(K), IXM(K), IYМ(K), IXYM(K)
Справочные данные о входных и выходных параметрах программы вычисления геометрических характеристик сечения приведены в табл. И.1. Таблица И.1 – Справочные данные о входных и выходных параметрах программы вычисления геометрических характеристик сечения
|

 , (И.1)
, (И.1) . (И.2)
. (И.2) ; (И.3)
; (И.3) ; (И.4)
; (И.4) . (И.5)
. (И.5) ; (И.6)
; (И.6)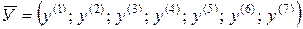 . (И.7)
. (И.7) ; (И.8)
; (И.8) ;
;  ; (И.9)
; (И.9) ;
;  . (И.10)
. (И.10)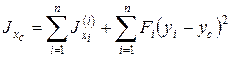 ; (И.11)
; (И.11) ; (И.12)
; (И.12) . (И.13)
. (И.13) окажется равным нулю, то формулы (И.11) и (И.12) дают значения главных центральных моментов инерции сечения.
окажется равным нулю, то формулы (И.11) и (И.12) дают значения главных центральных моментов инерции сечения. , находим угол наклона главных центральных осей (α;) к осям Сх, Cу и вычисляем J max и J min:
, находим угол наклона главных центральных осей (α;) к осям Сх, Cу и вычисляем J max и J min: ; (И.14)
; (И.14)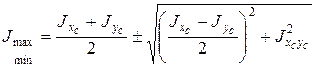 . (И.15)
. (И.15) ;
;  ;
; 

 Рисунок И.5б – Схема алгоритма определения геометрических
Рисунок И.5б – Схема алгоритма определения геометрических






