К.3 Расчет статически неопределимых стержней
Пример К.4. Определить реакцию шарнирно-подвижной опоры статически неопределимого стержня (рис. К.4). Решение: запишем аналитические выражения изгибающих моментов для сечений, отмеченных узловыми точками:
Рисунок К.4 – Схема стержня к примеру К.4
Воспользовавшись (К.9), составляем систему алгебраических уравнений:
Здесь неизвестные составляющие изгибающих моментов (зависящие от реакции R) перенесены в левые части уравнений. Общее число неизвестных (перемещения и реакция) превышает число уравнений. Из условий закрепления стержня следует, что перемещения Используя эти данные и учитывая, что
Здесь уже число уравнений равно числу неизвестных, и последние могут быть определены. Вычисляем реакцию опоры по правилу Крамера:
Точное значение реакции: Отсюда погрешность
Пример К.5. Раскрыть статическую неопределимость стержня с защемленными концами (рис. К.5).
Рисунок К.5 – Схема стержня к примеру К.5 Используя (К.9), составим следующую систему уравнений:
Из условия симметрии Используя эти данные, преобразуем исходную систему уравнений к виду:
Число уравнений равно числу неизвестных (перемещения и момент). Определяем момент:
При Точное значение момента [27]:
Погрешность
Пример К.6. Определить реакцию средней опоры двухпролетной балки при минимально допустимом числе интервалов разбиения (рис. К.6, а) Решение: вариант 1. При существующей взаимозависимости реакции опор (рис. К.6, б) моменты в сечениях, приходящихся на узловые точки 1, 2 и 3, определяются из выражений:
Учитывая, что перемещения опорных сечений равны нулю, запишем следующую систему уравнений:
а
б
в
Рисунок К.6 – Расчетные схемы к примеру К.6 Вычисляем определители системы:
Отсюда реакция опоры:
Вариант 2. Считаем неизвестными реакции опор Тогда
Составляем систему уравнений, в состав которой включаем дополнительное уравнение равновесия:
Вычисляем определители системы:
Отсюда, как и в первом варианте, имеем:
Рассмотренный подход к решению задачи позволяет значительно облегчить и, главное, формализовать процесс составления алгебраических уравнений. При этом можно не делать различия между статически определимыми и статически неопределимыми задачами, считая реакции опор неизвестными и доопределяя исходную систему алгебраических уравнений уравнениями равновесия.
|

 .
.

 равны нулю, а перемещение дополнительной узловой точки
равны нулю, а перемещение дополнительной узловой точки  . Последнее соотношение обеспечивает равенство нулю угла поворота в защемлении и следует из формулы (К.5), так как числитель в (К.5) равен нулю.
. Последнее соотношение обеспечивает равенство нулю угла поворота в защемлении и следует из формулы (К.5), так как числитель в (К.5) равен нулю. , преобразуем исходную систему уравнений к виду:
, преобразуем исходную систему уравнений к виду:
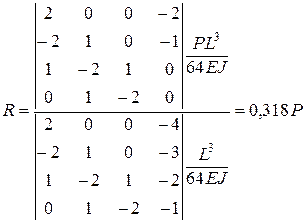 .
. [27].
[27]. .
. Решение: расчетная схема стержня симметрична, и
Решение: расчетная схема стержня симметрична, и  , то есть задача фактически один раз статически неопределима. Неизвестным является момент М.
, то есть задача фактически один раз статически неопределима. Неизвестным является момент М.
 . В защемлении
. В защемлении  (угол поворота, определяемый по формуле (К.3), равен нулю).
(угол поворота, определяемый по формуле (К.3), равен нулю).
 .
. имеем:
имеем:  .
. .
. .
.


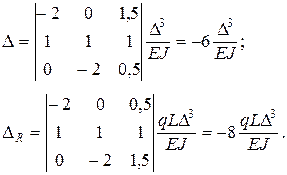
 .
. (рис. К.6, в).
(рис. К.6, в). .
.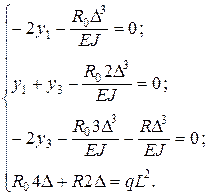
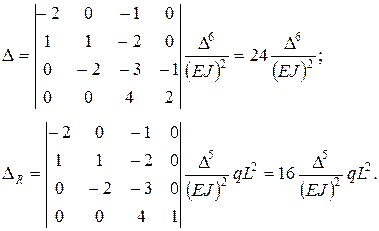
 .
.


