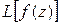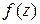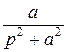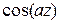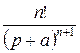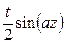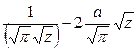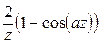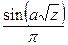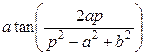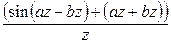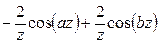ПРИЛОЖЕНИЕ Л
(справочное)
Преобразование Лапласа и его применение В теории изгиба стержней Операционное исчисление находит широкое применение при решении разнообразных задач механики и техники. В основе метода операционного исчисления лежит преобразование Лапласа, позволяющее заменять функции из «пространства оригиналов» функциями в «пространстве изображений», а также устанавливать соответствия в проведении «тождественных» операций над функциями в этих пространствах. Особый интерес представляет использование преобразования Лапласа и разработанных операций применительно к решению дифференциальных уравнений. Как известно, дифференциальное уравнение решается в два этапа: сначала находится общее решение, а затем его постоянные интегрирования определяются так, чтобы данное решение удовлетворяло начальным условиям. При решении же дифференциального уравнения посредством преобразования Лапласа начальные значения учитываются «автоматически», причем в случае нулевых начальных значений ход вычислений исключительно прост. Применение преобразования Лапласа позволяет сразу же решать неоднородное дифференциальное уравнение (во многих технических приложениях определяющее более важные практические результаты). Это обстоятельство избавляет от необходимости сначала решать однородное дифференциальное уравнение, а затем путем вариаций постоянных – неоднородное дифференциальное уравнение [25]. Показано, что решения известных дифференциальных уравнений изогнутой оси стержня, полученные методом операционного исчисления, записываются в виде универсальных уравнений с интегральными слагаемыми от распределенных нагрузок. На этапе выполнения прямого и обратного преобразований Лапласа, а также вычислений определенных интегралов в универсальных уравнениях общего вида использовались возможности символьной математики в рамках программы Mathcad. Л.1 Основные сведения по операционному исчислению Метод операционного исчисления базируется на использовании преобразования Лапласа, которое записывается в виде следующего соотношения:
Предполагается, что интеграл в правой части (Л.1) существует и сходится. Соотношение (Л.1) является интегральным преобразованием, позволяющим переходить от функции
Функцию Обратное преобразование Лапласа
однозначно определяет оригинал по своему изображению. Как правило, обратное преобразование производят путем сопоставления известных (табличных) соотношений «оригинал – изображение». При этом используются основные операции, позволяющие заменить «сложный» оригинал совокупностью простых, «табличных».
Л.1.1 Правила выполнения операций при преобразовании Лапласа
Операции с изображениями функций производятся по определенным правилам, которые формулируются в виде основных теорем. Названия теорем соответствуют операциям, которые выполняются над функциями оригинала (доказательства теорем опускаются [26]): Теорема сложения:
Теорема о свертке:
Теорема об интегрировании:
Теорема о дифференцировании:
Теорема о запаздывании:
Теорема о подобии:
Теорема о смещении:
Теорема об умножении:
Теорема о делении:
Л.1.2 Изображение единичной функции
По определению единичная функция
Найдем ее изображение. В соответствии с (Л.1) имеем:
Отсюда
Л.1.3 Изображение импульсной функции
Рассмотрим вспомогательную функцию «первого порядка»
Рисунок Л.1 – График функции
В пределе, когда
которая равна нулю для всех значений Для нахождения изображения импульсной функции
или
При Поскольку предел
то
Если
Л.1.4 Изображение импульсной функции
Рассмотрим вспомогательную функцию «второго порядка»
Рисунок Л.2 – График функции s 2 (z, h)
В пределе, когда
которая равна нулю для всех значений Предварительно найдем изображение вспомогательной функции В соответствии с [25] имеем:
или
Осуществляя предельный переход, получим:
и, следовательно,
Если
Л.1.5 Изображения ряда типовых функций
К типовым функциям отнесены функции, часто встречающиеся при решении задач изгиба стержней. Ряд этих функций и их изображения, которые являются дробно-рациональными функциями, представлены в таблице Л.1. Дополнительные сведения по прямому и обратному преобразованиям Лапласа можно найти в справочной литературе [25, 26].
Таблица Л.1 – Преобразования Лапласа для типовых функций
Л.1.6 Вычисления интегральных преобразований Лапласа
Современные ЭВМ позволяют использовать уникальные возможности программы Mathcad для проведения символьных вычислений. В результате символьного вычисления заданное (первоначальное) выражение преобразуется в новое (второе) выражение по известным математическим правилам. Это относится также к прямому и обратному преобразованиям Лапласа, осуществляемым в соответствии с формулами (Л.1) и (Л.2). Инструкции по ведению интегральных преобразований Лапласа в Mathcad изложены в [28]. Результаты выполнения некоторых преобразований Лапласа сведены в таблицу Л.2.
Таблица Л.2 – Преобразования Лапласа, выполненные в Mathcad
|

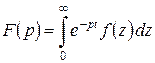 . (Л.1)
. (Л.1) к функции
к функции 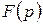 . Условное обозначение данного преобразования:
. Условное обозначение данного преобразования: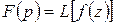 .
. (Л.2)
(Л.2)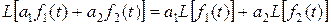 . (Л.3)
. (Л.3) . (Л.4)
. (Л.4) . (Л.5)
. (Л.5) . (Л.6)
. (Л.6)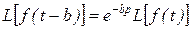 . (Л.7)
. (Л.7)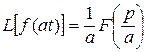 . (Л.8)
. (Л.8)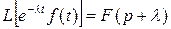 . (Л.9)
. (Л.9) . (Л.10)
. (Л.10) . (Л.11)
. (Л.11)
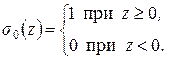 (Л.12)
(Л.12) .
. . (Л.13)
. (Л.13)
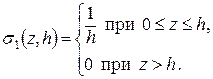

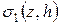
 , получаем искомую импульсную функцию первого порядка:
, получаем искомую импульсную функцию первого порядка: (Л.14)
(Л.14)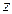 , кроме значения
, кроме значения 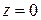 , где она обращается в бесконечность.
, где она обращается в бесконечность. предварительно найдем изображение вспомогательной функции
предварительно найдем изображение вспомогательной функции 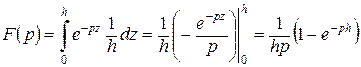 ,
, .
.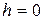 найдем изображение импульсной функции
найдем изображение импульсной функции 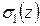 .
. ,
, . (Л.15)
. (Л.15) имеет размерность единицы длины, например «метр», то размерность импульсной функции
имеет размерность единицы длины, например «метр», то размерность импульсной функции 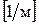 .
.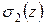


 (Л.16)
(Л.16) .
. ,
,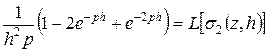 .
.
 . (Л.17)
. (Л.17) будет
будет 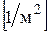 .
.