Л.2 Вывод универсальных уравнений изогнутой оси стержня
Непосредственное интегрирование дифференциальных уравнений изогнутой оси стержня сопряжено в ряде случаев с большими трудностями, обусловленными необходимостью определять постоянные интегрирования. Для стержня, имеющего n участков, находятся 2 n постоянных интегрирования из решения 2 n уравнений [2]. Метод начальных параметров свободен от этого недостатка. Число постоянных интегрирования сводится к двум при любом количестве участков стержня. Запись уравнения изогнутой оси стержня (универсального уравнения) по этому методу производится по известному алгоритму [1, 3], который определяет структуру и число членов уравнения, соответствующих действующим на стержень нагрузкам. Но если на стержень действует распределённая нагрузка, изменяющаяся по произвольному закону, то получение решения значительно усложняется. Операционное исчисление позволяет избежать трудностей непосредственного интегрирования дифференциальных уравнений изогнутой оси стержня и, сохраняя все преимущества метода начальных параметров, обеспечивает простой алгоритм получения решения и в том случае, если на стержень действуют распределенные нагрузки, изменяющиеся по произвольному закону. Для определения изогнутой оси стержня будем использовать следующие исходные дифференциальные уравнения [29]:
где
Л.2.1 Решение дифференциального уравнения второго порядка
Изображение искомого решения дифференциального уравнения (Л.18) с учетом теоремы о дифференцировании (Л.6) и начальных условий определяется уравнением вида
где Поскольку оригиналы функций, входящих в правую часть уравнения (Л.20), известны (1 и
или В уравнениях (Л.21) и (Л.22) принято, что Если применить преобразования Лапласа к решению исходного дифференциального уравнения (Л.18), представленного в виде
то получим уравнение для определения углов поворота
К уравнению (Л.23) приходим также, беря производную от левой и правой частей уравнения (Л.21) по переменной По аналогии, дифференцируя уравнение (Л.22), получим:
где В случае, когда жесткость
или
где
Л.2.2 Решение дифференциального уравнения четвертого порядка
Чтобы воспользоваться дифференциальным уравнением (Л.19), необходимо определить «интенсивность» сосредоточенной силы и момента, и, таким образом, включить их в состав распределённой нагрузки. Теоретически сосредоточенную силу можно представить как распределённую нагрузку, действующую на площадке, размеры которой стремятся к нулю. При этом интенсивность распределенной нагрузки должна увеличиваться до бесконечности. Такое представление сосредоточенной силы можно записать математически в виде произведения силы на импульсную функцию первого порядка:
Составим произведение сосредоточенного момента на импульсную функцию второго порядка:
Это произведение теоретически можно рассматривать как распределённую нагрузку, действующую на балку в точке приложения момента и создающую такой же эффект действия, что и момент. Следовательно, произведения (Л.27 а) и (Л.27 б) можно подставлять в правую часть уравнения (Л.19). Рассмотрим расчетную схему нагруженного стержня (рис. Л.3). Здесь имеется распределенная нагрузка Момент, сила и распределенная нагрузка считаются положительными. Исходное дифференциальное уравнение (Л.19) с учётом заданных нагрузок записывается в виде:
Рисунок Л.3 – Схема нагружения стержня
Воспользовавшись изображением импульсных функций (Л.15) и (Л.17), а также теоремами о сложении (Л.3) и запаздывании (Л.7), запишем изображение правой части дифференциального уравнения (Л.19):
Учитывая полученное изображение и применяя теорему о дифференцировании (Л.6) к (Л.28), найдем изображение уравнения изогнутой оси стержня:
Осуществим обратное преобразование Лапласа. Согласно теореме о свертке (Л.4), оригинал, или уравнение изогнутой оси стержня, записывается в виде:
или
где Чтобы получить уравнение для определения углов поворота Допускаются следующие формы записи данного уравнения:
и
Вычисляя значения прогибов и углов поворота на одном из участков стержня Когда на стержень действует несколько моментов, сил или распределенных нагрузок (а также реакции связей), в данные уравнения включаются соответствующие им слагаемые. По существу, уравнения (Л.29) – (Л.32) являются универсальными уравнениями общего вида и отличаются от известных универсальных уравнений наличием интегральных слагаемых. В таблице Л.3 представлены выведенные в этом разделе универсальные уравнения.
Таблица Л.3 – Универсальные уравнения для определения прогибов
Продолжение таблицы Л.3
При записи универсальных уравнений (Л.29) – (Л.32) учтено, что внутренние силовые факторы в начале координат
Л.2.3 Символьное вычисление определенных интегралов
Программа Mathcad позволяет производить символьные вычисления определенных интегралов. В результате данных вычислений записывается математическое выражение, определяемое через первообразную функцию в соответствии с основной теоремой интегрального исчисления [26], или числовой ответ. Инструкции по символьному вычислению определенных интегралов в Mathcad изложены в [3]. Ниже приведены некоторые примеры интегрирования с использованием возможностей символьной алгебры:
|

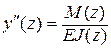 ; (Л.18)
; (Л.18) , (Л.19)
, (Л.19)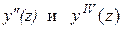 – вторая и четвертая производные от функции
– вторая и четвертая производные от функции  , определяющей уравнение изогнутой оси стержня;
, определяющей уравнение изогнутой оси стержня;  – изгибающий момент, как внутренний силовой фактор;
– изгибающий момент, как внутренний силовой фактор;  – внешняя распределенная нагрузка;
– внешняя распределенная нагрузка; 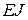 – жесткость стержня. В случае, если жесткость стержня изменяется по длине стержня, следует использовать дифференциальное уравнение (Л.18).
– жесткость стержня. В случае, если жесткость стержня изменяется по длине стержня, следует использовать дифференциальное уравнение (Л.18).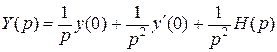 , (Л.20)
, (Л.20) – изображение решения;
– изображение решения; 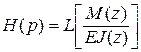 – изображение правой части дифференциального уравнения (Л.18);
– изображение правой части дифференциального уравнения (Л.18);  – перемещение и угол поворота в начале координат.
– перемещение и угол поворота в начале координат.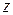 являются оригиналами функций
являются оригиналами функций  ), то, воспользовавшись теоремой о свертке (Л.4), найдем:
), то, воспользовавшись теоремой о свертке (Л.4), найдем: , (Л.21)
, (Л.21) . (Л.22)
. (Л.22)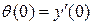 .
. ,
,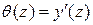 :
: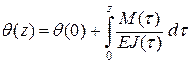 . (Л.23)
. (Л.23) (Л.24)
(Л.24) – момент;
– момент; 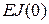 – жесткость стержня в начале координат.
– жесткость стержня в начале координат.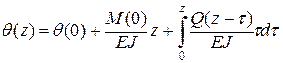 , (Л.25)
, (Л.25) , (Л.26)
, (Л.26) и
и  – поперечные силы.
– поперечные силы.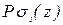 . (Л.27 а)
. (Л.27 а) . (Л.27 б)
. (Л.27 б) .
. (Л.28)
(Л.28)
 .
.
 (Л.29)
(Л.29) (Л.30)
(Л.30) – поперечная сила в начале выбранной системы координат
– поперечная сила в начале выбранной системы координат  .
. (Л.31)
(Л.31) (Л.32)
(Л.32) , следует учитывать только те слагаемые в уравнениях (Л.29) – (Л.32), которые располагаются слева от черты с нижним индексом данного участка. При переходе на пятый участок стержня учитываются все слагаемые уравнений, причем верхний предел интегрирования
, следует учитывать только те слагаемые в уравнениях (Л.29) – (Л.32), которые располагаются слева от черты с нижним индексом данного участка. При переходе на пятый участок стержня учитываются все слагаемые уравнений, причем верхний предел интегрирования  .
.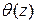 сечений стержня
сечений стержня 1.1. Жесткость стержня изменяется по произвольному закону:
1.1. Жесткость стержня изменяется по произвольному закону:
 ;
;
 ;
;
 .
.
 ;
;
 ;
;
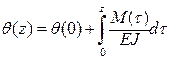 ;
;
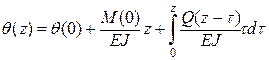 ;
;
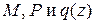 (
( ):
):
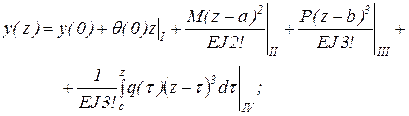
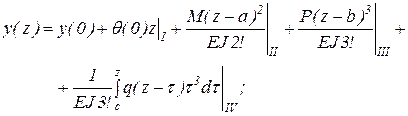

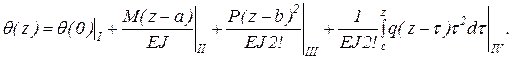
 могут быть причислены к внешним заданным нагрузкам.
могут быть причислены к внешним заданным нагрузкам.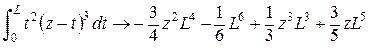 ;
; ;
; ;
; –––––
––––– ;
; .
.


