К.2 Расчет статически определимых стержней
Пример К.1. Для симметричной балки (рис. К.1.) найти прогиб в узловых точках 1 и 2, а также угол поворота опорного сечения балки. Решение: последовательно записывая уравнение (К.10) относительно узловых точек 1 и 2, получим систему:
где
Рисунок К.1 – Схема к примеру К.1
Значения прогибов Поскольку из формулы (К.6)
то С учетом значений
Отсюда При
Погрешность составляет не более 7 %:
В разобранном примере длина стержня искусственно увеличивалась, и вводились дополнительные узловые точки, которые использовались для удовлетворения краевым условиям (геометрическому – Необходимость в этом отпадает, если алгебраическая система уравнений относительно перемещений в узловых точках составляется по алгоритму, определенному уравнением (К.9). Для данного случая получим следующую систему уравнений:
или после преобразований:
Характерно, что уравнения данной системы обращаются в тождество при вышенайденных значениях Чтобы определить угол поворота опорного сечения, достаточно разделить значение перемещения в узловой точке 1 на
Точное значение угла поворота
то есть погрешность не превышает 7 %:
При решении следующей задачи оценим точность получаемых решений при уменьшении длины интервала разбиения. Пример К.2. Определить перемещение в середине пролета шарнирно закрепленной балки длиной
а
б Рисунок К.2 – Схемы к примеру К.2 Решение: воспользуемся уравнением (К.9). Для схемы а имеем:
или
Складывая левые и правые члены этих уравнений, находим:
Погрешность Для схемы б составим систему трех уравнений:
Перемещение
Поскольку
Погрешность
то есть по сравнению с первым вариантом расчета уменьшилась вдвое. Пример К.3. Для консольной балки (рис. К.3) определить перемещение свободного конца при интервале разбиения
Решение: воспользуемся уравнением (К.9) и, записывая его для узловых точек 1, 2 и 3, образуем систему:
Рисунок К.3 – Схема к примеру К.3
Из геометрических краевых условий в защемлении находим, что В правых частях уравнений системы изгибающие моменты определяются из выражений:
Исключаем “лишние” неизвестные
Определители системы:
Отсюда
Расчетные значения прогиба практически совпадают с точным. Погрешность
|


 и
и  .
.
 находятся из краевых условий. Для шарнирного закрепления
находятся из краевых условий. Для шарнирного закрепления  и
и  .
. ,
, .
. и
и  исходная система уравнений запишется в виде:
исходная система уравнений запишется в виде:
 и
и  .
. прогиб
прогиб  , и его можно сопоставить с точным значением:
, и его можно сопоставить с точным значением: .
. .
. ).
).

 и
и  .
. :
: .
. ,
, .
. при интервалах разбиения
при интервалах разбиения  (рис. К.2, б). Сопоставить расчетное значение перемещения с точным:
(рис. К.2, б). Сопоставить расчетное значение перемещения с точным:  .
.



 .
.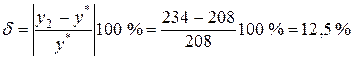 .
.
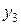 находим по правилу Крамера [26]:
находим по правилу Крамера [26]: .
. .
. ,
, . Сопоставить расчетное значение прогиба с точным:
. Сопоставить расчетное значение прогиба с точным: .
.

 , а
, а  (
( и, соответственно,
и, соответственно,  ).
).
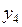 в исходной системе уравнений и преобразуем ее к виду:
в исходной системе уравнений и преобразуем ее к виду:
 ;
; .
. .
. .
.


