К.1 Основы метода конечных разностей
Для получения приближенных значений прогибов (перемещений) и углов поворотов при изгибе стержня можно воспользоваться методом конечных разностей [23]. Этот метод позволяет для исходного дифференциального уравнения изогнутой оси стержня
или
составить конечно-разностные уравнения и тем самым образовать систему линейных алгебраических уравнений относительно неизвестных перемещений в узловых точках. Алгоритмы решения таких систем хорошо отработаны, и имеются готовые программы для ЭВМ. Использование современных ЭВМ обеспечивает не только оперативное получение решений и приемлемую их точность при увеличении порядка системы практически до нескольких тысяч, но и вычисление коэффициентов определителей системы по исходным данным – нагрузкам, геометрическим размерам и краевым условиям стержня. Однако при постановке и решении задач изгиба, связанных с учетом неоднородности внутренней структуры стержней, краевых условий, температурных полей и т. п. не всегда возможно использовать имеющиеся готовые программы и приходится разрабатывать специальные программы. Ниже на примерах решения конкретных задач изгиба стержней показаны основные правила и особенности составления конечно-разностных уравнений, а также определения неизвестных перемещений, углов поворотов и реакций опор. Соответствующие приемы решения типовых задач можно использовать при разработке алгоритмов и программ специального наз-начения. К.1.1 Вывод центральных конечно-разностных формул
Пусть уравнение изогнутой оси стержня описывается функцией Согласно теореме Тейлора, значения функции в узловых точках с координатами
где D – расстояние между узловыми точками при равных интервалах разбиения длины стержня. Если ограничиться тремя членами ряда в (К.3) и (К.4), то, вычитая и складывая их, найдем первую и вторую производные в i -й узловой точке:
Воспользуемся этими формулами для нахождения третьей и четвертой производных:
которые после исключения из них согласно (К.6) вторых производных и приведения подобных слагаемых запишутся в виде:
В полученных формулах наблюдается “симметрия индексов” относительно узловой точки как центра. Поэтому эти формулы принято называть центральными конечными разностями. При необходимости можно использовать и односторонние формулы, в которых производные определяются через правые (или левые) ординаты относительно узловой точки, а также формулы, в которых учитывается неравномерность шага разбиения длины стержня [24].
|

 (К.1)
(К.1) (К.2)
(К.2) .
.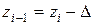
 и
и  могут быть выражены через производные в i -й узловой точке с координатами
могут быть выражены через производные в i -й узловой точке с координатами  степенными ря-дами:
степенными ря-дами: ; (К.3)
; (К.3) , (К.4)
, (К.4) и т.д.;
и т.д.; ; (К.5)
; (К.5) . (К.6)
. (К.6) ;
; ,
, ; (К.7)
; (К.7) . (К.8)
. (К.8)


