Л.3 Примеры определения прогибов и углов поворота
В примерах непосредственно использовались универсальные уравнения общего вида, выведенные на основе метода операционного исчисления. Во всех расчетных схемах стержня (рис. Л.4 – Л.13) прогибы определяются в сечении А, а углы поворота – в сечении Б. Пример Л.1
 

Рисунок Л.4 – Расчетная схема к примеру Л.1
Запишем начальные условия: Согласно (Л.29) и (Л.31), имеем:
Отсюда Пример Л.2


Рисунок Л.5 – Расчетная схема к примеру Л.2
Момент. Поперечная сила Начальные условия: Воспользовавшись уравнением (Л.30) и учитывая, что прогиб определяется на консольной части стержня, запишем:
При координате
Угол поворота определим по уравнению (Л.32), в соответствии с которым:
и
Пример Л.3
Рисунок Л.6 – Расчетная схема к примеру Л.3 Момент Поперечная сила Начальные условия: В соответствии с (Л.29) и (Л.31) имеем:
Из первого уравнения определим прогиб:
а из второго – угол поворота: Пример Л.4

Рисунок Л.7 – Расчетная схема к примеру Л.4
Реакция левой опоры: .
Известные начальные условия: Угол поворота в начале координат найдем из условия равенства нулю прогиба стержня в месте его присоединения к шарнирно-подвижной опоре. Из уравнения (Л.29) следует, что
Поскольку при координате
Отсюда Подставляя это выражение в уравнение изогнутой оси стержня, определим прогиб:
Примечание: решение данной задачи с использованием уравнения (Л.30) недопустимо, так как информация о смещении постоянной распределенной нагрузки «теряется».
|




 ;
;  ;
;  ;
; 
 .
. ;
; .
. ;
;  .
.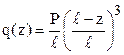

 .
. ;
;  .
. .
. определим прогиб:
определим прогиб:

 .
.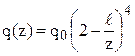





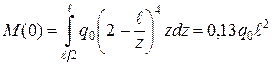 .
. .
.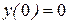 ;
;  ;
; 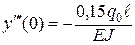 .
. ;
; .
. ,
, .
.




 .
. .
. , то
, то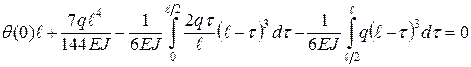 .
. .
. .
.


