Дифференциальное уравнение, описывающее вынужденные колебаниянаших двух систем будет иметь один и тот же вид:
Решение дифференциального уравнения Решение дифференциального уравнения вынужденных колебаний - ξ(t) - состоит из двух слагаемых:
здесь ξ1(t) - общее решение однородного уравнения, т.е. уравнения с нулем в правой части (см. 14.4.5.), ξ2(t) - частное решение неоднородного уравнения, т.е. уравнения с ненулевой правой частью - (14.5.5)
здесь - ξ1(t) убывает с течением времени и его роль существенна при переходных процессах. Стационарное, установившееся значение ξ(t) определяется, в основном, слагаемым ξ2(t). Наша задача - найти ξ2(t).
Частное решение неоднородного уравнения Частное решение неоднородного уравнения - ξ2(t). Ищем ξ2(t) в виде гармонической функции изменяющейся с частотой внешнего воздействия ω;:
Первая и вторая производные от этой функции также будут гармоническими функциями, изменяющиеся с частотой ω;. Значит, в уравнении 14.5.3.5, в левой его части, будет сумма трех гармонических функций одинаковой частоты, справа - гармоническая функция той же частоты, т.е. сумма трех колебаний одной частоты равна четвертому колебанию той же частоты. Задачу о сложении колебаний мы решим методом векторных диаграмм (14.3.1.), для этого
|
,
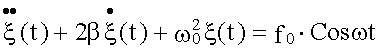
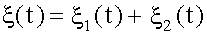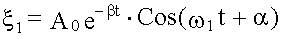- из (14.4.6),
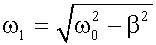- частота затухающих колебаний.
.
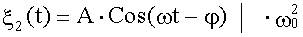и 
, после нахождения этих производных, запишем с помощью функции косинуса:
.
