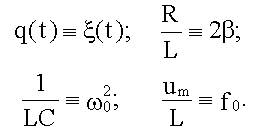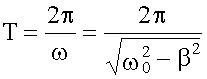 .
.
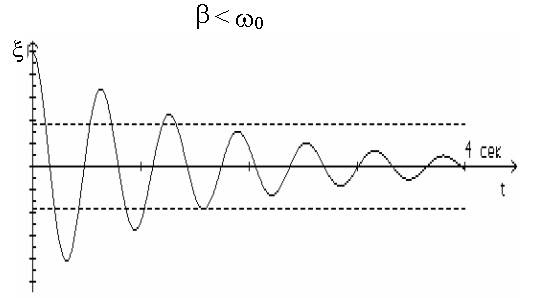
График затухающих колебаний
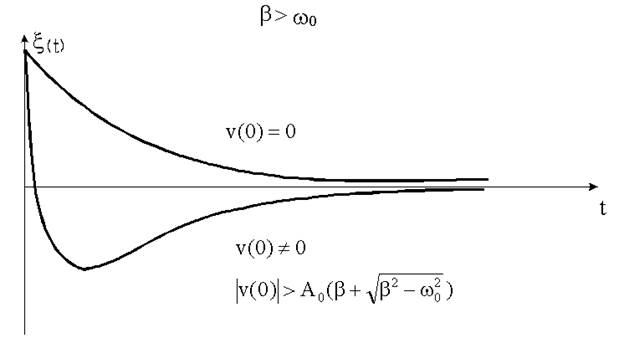
Переход к апериодическому движению
При увеличении коэффициента затухания β; период затухающих колебаний (14.4.9) растет, при β → ω0 период T → ∞;. При β > ω0 периодическое решение у дифференциального уравнения затухающих колебаний отсутствует:
Логарифмический декремент затухания
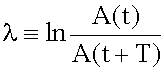 ,
,
подставим A(t) = A0-βt.
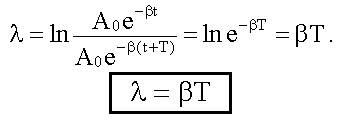 .
.
Время релаксации
Время релаксации - это время τ, за которое амплитуда уменьшилась в e=2,7... раз, т.е. 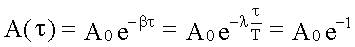 , тогда
, тогда 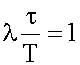 .
.
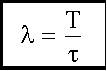 .
.
Т.к. 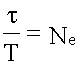 - число колебаний за время, то:
- число колебаний за время, то:
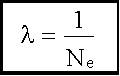 .
.
Добротность
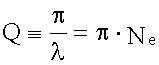 .
.
Вынужденные колебания
Вынужденные колебания - это колебания, происходящие под действием периодического внешнего воздействия.
| 14.5.1. Колеблющиеся системы
|
| 
|
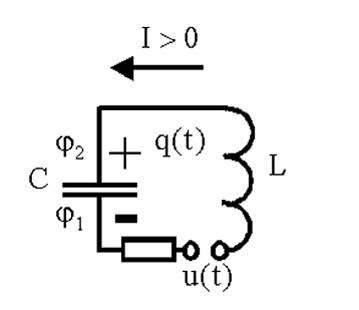
В контур включен последовательно источник переменного напряжения, изменяющегося по гармоническому закону 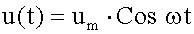 . .
| На грузик m действует внешняя сила, изменяющаяся по гармоническому закону 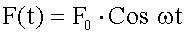 . .
|
| 14.5.2. Законы движения
|
| Закон Ома для неоднородного участка цепи:
| Второй закон Ньютона:
|
 . .
|  . .
|
| 14.5.3. Применение законов движения
|
| Применим законы движения к изучаемым системам:
|
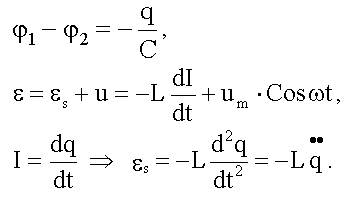
| 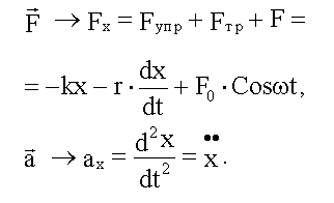
|
| Получим дифференциальные уравнения:
|
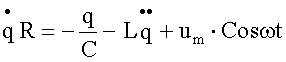 , ,
| 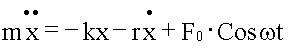 . .
|
| Приведем уравнения к каноническому виду - делим на коэффициент при старшей производной и переносим все члены уравнения, содержащие неизвестную функцию, в левую часть:
|
 ; ;
| 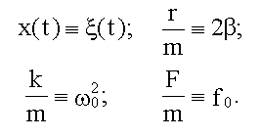 . .
|
| 14.5.4. Введем обозначения
|
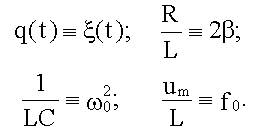
| 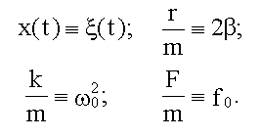
|

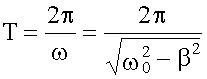 .
.

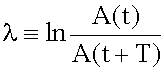 ,
,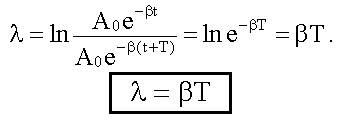 .
.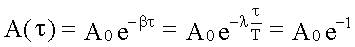 , тогда
, тогда 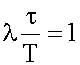 .
.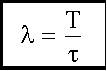 .
.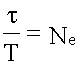 - число колебаний за время, то:
- число колебаний за время, то: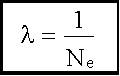 .
.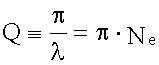 .
.

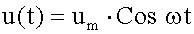 .
.
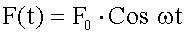 .
.
 .
.
 .
.
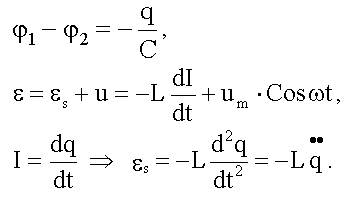
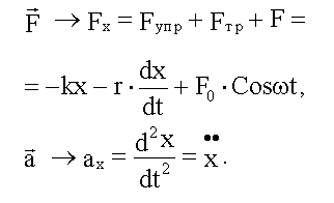
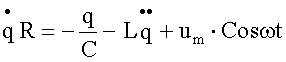 ,
,
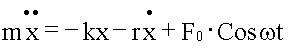 .
.
 ;
;
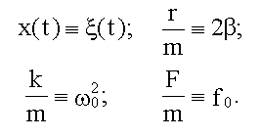 .
.