Векторная диаграмма
Изобразим эти колебания с помощью векторов (14.3.1.), амплитуды которых получаются после умножения
В отличие от (14.3.2) вправо направим вектор длиной ω20A, изображающий функцию ω20A · Cos(ωt - φ), начальная фаза которой равна "минус фи".
Резонанс Т.к. то
Таким образом, амплитуда вынужденных колебаний изменяется с изменением частоты внешнего воздействия. При определенной частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота - ωрез - резонансной. Для определения ωрез исследуем функцию A(ω;) на максимум, для этого достаточно найти минимум знаменателя у выражения A(ω). Возьмем от него производную по и приравняем к нулю:
откуда:
При 2β2 > ω20 резонанс отсутствует (ωрез - мнимое число).
Амплитуда при резонансе Амплитуда при резонансе получается при подстановке найденного выражения ωрез в формулу для A(ω;).
При β << ω0:
При ω = 0 отклонение системы от положения равновесия
Найдем отношение Aрез / A0 при условии β << ω0:
здесь Q - добротность. Добротность показывает (при β << ω0) во сколько раз амплитуда при резонансе больше смещения при ω = 0.
Резонансные кривые График зависимости A(ω) при различных β; носят название резонансных кривых.
β1 < β2 < β3, 2β23 > ω20, в этом случае резонанса нет.
|

 на 2β;, а - ξ на ω20.
на 2β;, а - ξ на ω20. .
.
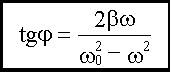
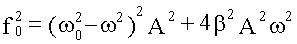 ,
,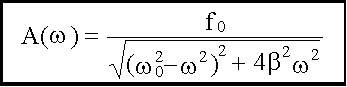 .
.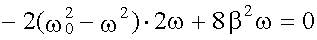 ,
,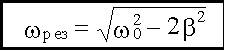 .
. .
. .
. .
. ,
,



