Волновое число, симметричная форма уравнения волны
Введем
Тогда
При такой записи координата х и время t входят в уравнение волны симметрично. Связь волнового числа с длиной волны
Уравнение плоской волны, распространяющейся в произвольном направлении. Волновой вектор
здесь
Волновое уравнение Применяя второй закон Ньютона (4.6) к упругой среде, можно получить дифференциальное уравнение в частных производных, решением которого будет уравнение волны. Логическая схема этого вывода такова:
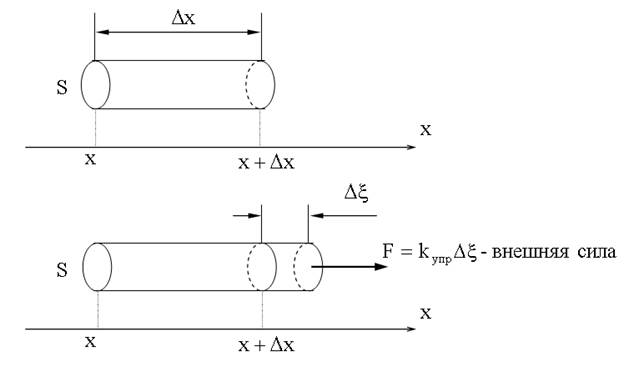
Вывод закона Гука для бесконечно малого упругого стержня Выделим элемент упругого стержня, длиной Δx.
Закрепим левую часть этого элемента (второй рисунок), правую сместим на величину Δξ; вдоль оси x. Здесь коэффициент kупр, характеризующий упругость стержня, зависит от материала стержня, его длины и площади сечения. Нормальное напряжение и относительная деформация Введем:
При Δx → 0
Перепишем
или
Модуль Юнга Величина
|

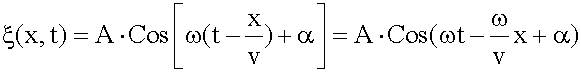 .
. - волновое число.
- волновое число. .
. .
.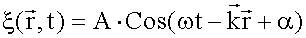 ,
, - волновой вектор,
- волновой вектор,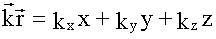 - скалярное произведение волнового вектора и радиус-вектора.
- скалярное произведение волнового вектора и радиус-вектора.
 - закон Гука.
- закон Гука. - нормальное напряжение,
- нормальное напряжение, - относительная деформация.
- относительная деформация. .
.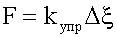 , выразив F и Δξ; через σ; и ε;:
, выразив F и Δξ; через σ; и ε;: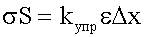
 .
. не зависит от длины и сечения стержня, она определяется только упругими свойствами материала, ее называют модулем Юнга материала:
не зависит от длины и сечения стержня, она определяется только упругими свойствами материала, ее называют модулем Юнга материала: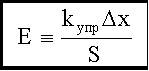 .
.


