Плоская и сферическая волны
Плоская волна - волновые поверхности - плоскости. Сферическая волна - волновые поверхности - сферы. В общем случае форма волновых поверхностей может быть любой. Длина волны - это расстояние, на которое распространяется волна за один период колебаний.
Так как (14.1.1.3) то Уравнение плоской волны. Пусть в начале координат находится твердая плоскость, которая колеблется по гармоническому закону и вынуждает частицы упругой среды, находящейся рядом с ней, колебаться по этому же закону. Направим ось x перпендикулярно этой плоскости. Тогда вдоль этой оси будет распространяться плоская гармоническая продольная волна. Наша задача - найти
Колебания до волновой поверхности, удаленной от начала координат на расстояние x, дойдут через время
Фаза волны - это аргумент у косинуса в уравнении волны, т.е.
Фаза плоской волны зависит от двух переменных - x и t. Фазовая скорость - это скорость перемещения в пространстве поверхности, вдоль которой фаза волны (15.2.1) остается постоянной, т.е.
Найдем производную от этого выражения по времени:
откуда искомая фазовая скорость волны:
Уравнение плоской волны, распространяющейся в направлении, противоположном оси x:
Из (15.2.2) для этой волны:
|
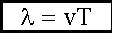см. (3.9),
,
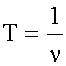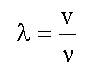или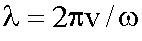 
.
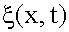- уравнение волны, если задано 
.
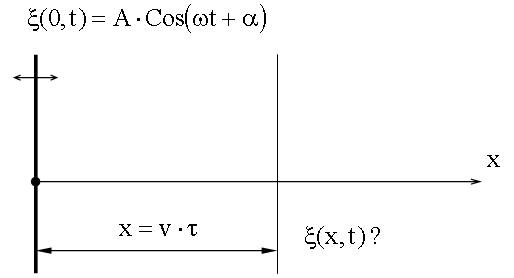
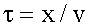, значит уравнение волны
.
,
.
,
.
.
.
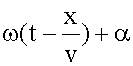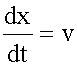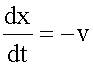