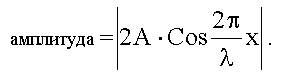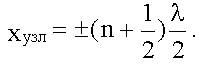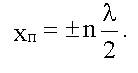Плотность энергии упругой волны
Плотность энергии упругой гармонической волны
Среднее по времени значение плотности энергии упругой гармонической волны
Поток энергии
Плотность потока энергии
Вектор Умова - связь плотности потока энергии с плотностью энергии упругой волны
Интенсивность волны - это среднее по времени от модуля вектора плотности потока энергии:
Для гармонической волны:
Стоячие волны При наложении двух встречных плоских волн с одинаковой амплитудой возникает колебательный процесс, называемый стоячей волной. При этом переноса энергии не происходит. Уравнение стоячей волны Для волны, бегущей по оси x:
Для волны, бегущей против оси x:
Для простоты мы положили равным нулю значение начальных фаз этих волн. Сумма этих уравнений и дает уравнение стоячей волны:
Амплитуда стоячей волны - это модуль выражения, стоящего перед множителем Cosωt, т.е.
Узлы и пучности Поверхность, где амплитуда колебаний равна нулю, называют узлами стоячей волны. Для узлов:
Следовательно, координаты узлов:
Поверхность, где амплитуда колебаний достигает максимума, называют пучностями стоячей волны. Для пучностей:
Координаты пучностей:
|
.
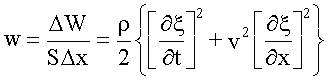, это известно из математики, значит:
.
.
.
.
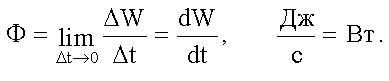
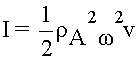, см. (15.2.3), (15.2.4), (15.2.5).
