Статичний спосіб визначення коефіцієнтів і вільних членів системи канонічних рівнянь та їх перевірка
Коефіцієнти й вільні члени системи канонічних рівнянь методу переміщень визначаються, виходячи з їхнього фізичного запису, тобто вони являють собою реакції, що виникають у відповідній додатковій в’язі основної системи від одиничного значення невідомого переміщення або зовнішнього навантаження. Додатні напрями реакцій збігаються з напрямами відповідних невідомих переміщень
а) основна система; б) еквівалентна система; в) епюра Рисунок 1.8 – Рама 1 та епюри згинальних моментів
а) основна система; б) еквівалентна система; в) епюра Рисунок 1.9 – Рама 2 та епюри згинальних моментів 1. Реактивні моменти у введених рухомих затисненнях жорстких вузлів; 2. Реакції у введених додаткових опорних стержнях. Коефіцієнти та вільні члени системи канонічних рівнянь визначаються способом перемноження епюр (формула Мора), або статичним способом. 1.6.1 Реактивні моменти у введених рухомих затисненнях Для визначення реактивних моментів статичним способом необхідно виокремити вузол з епюри згинальних моментів відповідного одиничного або вантажного стану із введеним рухомим затисненням. До цього вузла прикладається невідомий реактивний момент у затисненні, напрямок якого співпадає з напрямком відповідного переміщення, а також згинальні моменти в перерізах стержнів відповідної епюри згинальних моментів. Складається рівняння рівноваги цього виокремленого вузла та визначаємо реактивний момент ( Так для рами на рис. 1.8 (а) коефіцієнт
Коефіцієнт
Коефіцієнт
Вільний член
На рис. 1.11 (а, б, в, г) наведено вузол 2, рівновагу якого слід розглянути для визначення коефіцієнтів і вільного члена другого рядка системи канонічних рівнянь, що являють собою реактивні моменти в рухомому затисненні, вузла 2 основної системи (рис. 1.4, б), від одиничних невідомих переміщень
а) визначення Рисунок 1.10 – Визначення одиничних коефіцієнтів та вільних членів
а) визначення Рисунок 1.11 – Визначення одиничних коефіцієнтів та вільних членів 1.6.2 Реакції у введених додаткових опорних стержнях До другого виду коефіцієнтів і вільних членів системи канонічних рівнянь методу переміщень належать такі, що за фізичним змістом є силовими реакціями в додаткових опорних стержнях, що введені при створенні основної системи. Для обчислення їхньої величини статичним способом необхідно розглянути умови рівноваги відокремленого фрагмента основної системи. Для визначення положення перетину, що виокремлює потрібний фрагмент, зручно скористатися картиною переносів шарнірної системи. Перетин повинен проходити через додатковий стержень, в якому обчислюється реакція, а також через усі стержні основної системи, які зазнають перекосів від примусового поступального переміщення в напрямі цього додаткового стержня. Зауважимо, що стержень доцільного перерізати нескінченно близько до одного з його кінців. Щоб побудувати картини перекосів шарнірної схеми для рами, наведеної на рис. 1.1 (б) від невідомого поступального переміщення Для побудови картини переносів шарнірної схеми для рами, що зображена на рис 1.2 (б) від невідомого поступального переміщення Для визначення реакцій у додатковому опорному стержні до відокремленого фрагмента слід прикладати всі сили, що діють на нього, у тому числі зусилля в перерізах. Поперечні сили в перерізах можна отримати з епюр згинальних моментів відповідного одиничного або вантажного стану за формулою:
Шукана реакція в додатковому опорному стержні визначається з рівняння рівноваги у вигляді суми проекцій на вісь додаткового стержня. Для прикладу обчислюємо одиничні коефіцієнти й вільний член третього рядка, системи канонічних рівнянь для розрахунку рами, що зображена на рис. 1.8 (а). Коефіцієнт
Отже, поперечна сила Q від’ємна, тому прикладаємо її у перерізі стержня таким чином, щоб вона поверталась навколо вузла 1 проти руху годинникової стрілки. Коефіцієнт Для його визначення вирізаємо той самий фрагмент основної системи (рис. 1.8, б) і прикладаємо до нього шукану реакцію Складаємо рівняння рівноваги:
Коефіцієнт Для його визначення вирізаємо той самий фрагмент основної системи (рис. 1.8, б) і прикладаємо до нього шукану реакцію Складаємо рівняння рівноваги:
Вільний член
Коефіцієнти та вільні члени канонічних рівнянь можна визначити й за допомогою формули Мора (спосіб перемноження епюр). Визначені одиничні коефіцієнти та вільні члени підставляємо в систему канонічних рівнянь, яка має на головній діагоналі додатні коефіцієнти, побічні коефіцієнти є симетричними відносно головної діагоналі, і це може розглядатись як побіжна перевірка обчислення коефіцієнтів системи рівнянь.
а) перевірка 1; б) перевірка 2; в) перевірка 3; г) перевірка 4 Рисунок 1.12 – Перевірка правильності визначення одиничних коефіцієнтів та вільних членів 1.6.3 Перевірка коефіцієнтів та вільних членів канонічних рівнянь Запишемо систему канонічних рівнянь для рами, що зображена на рис. 1.8 (а). Для перевірки правильності обчислення коефіцієнтів будується сумарна одинична епюра згинальних моментів від одночасної дії всіх основних невідомих, які дорівнюють одиниці:
Порядкова перевірка одиничних коефіцієнтів полягає в почерговому перемноженні сумарної одиничної епюри
Універсальна перевірка одиничних коефіцієнтів полягає в перемноженні сумарної одиничної епюри
Стовпцева перевірка вільних членів канонічних рівнянь полягає в перемноженні сумарної одиничної епюри
Основною системою методу сил називають геометрично незмінну й статично визначувану систему, яка одержана із заданої статично невизначуваної системи відкидання «зайвих» (надлишкових) в’язей.
|

 . Зазначені реакції поділяються на два види.
. Зазначені реакції поділяються на два види.
 ; г) епюра
; г) епюра 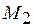 ; д) епюра
; д) епюра  ; е) епюра
; е) епюра 

 ).
). – це реактивний момент у рухомому затисненні вузла 1 основної системи (рис. 1.4, б) від одиничного кута повороту
– це реактивний момент у рухомому затисненні вузла 1 основної системи (рис. 1.4, б) від одиничного кута повороту  в першому одиничному стані (рис. 1.8, в). Складаємо рівняння рівноваги цього виокремленого вузла 1 (рис. 1.10, а):
в першому одиничному стані (рис. 1.8, в). Складаємо рівняння рівноваги цього виокремленого вузла 1 (рис. 1.10, а):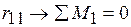 ;
; ;
;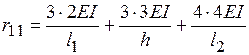 .
. – це реактивний момент у рухомому затисненні вузла 1 основної системи (рис 1.10, б) від одиничного кута повороту
– це реактивний момент у рухомому затисненні вузла 1 основної системи (рис 1.10, б) від одиничного кута повороту  , тобто в другому одиничному стані (рис. 1.8, г). Виокремлюємо вузол 1 з епюри
, тобто в другому одиничному стані (рис. 1.8, г). Виокремлюємо вузол 1 з епюри  і складаємо рівняння його рівноваги (рис. 1.10, б):
і складаємо рівняння його рівноваги (рис. 1.10, б): ;
; .
. – це реактивний момент у рухомому затисненні, вузла 1 основної системи (рис. 1.4, б), від одиничного поступального переміщення
– це реактивний момент у рухомому затисненні, вузла 1 основної системи (рис. 1.4, б), від одиничного поступального переміщення  , тобто в третьому одиничному стані (рис. 1.8, д). Виокремлюємо вузол 1 з епюри
, тобто в третьому одиничному стані (рис. 1.8, д). Виокремлюємо вузол 1 з епюри  і складаємо рівняння його рівноваги (рис. 1.10, в):
і складаємо рівняння його рівноваги (рис. 1.10, в): ;
; .
. − це реактивний момент у рухомому затисненні вузла 1 основної системи (рис. 1.4, б), від зовнішнього навантаження, тобто у вантажному стані (рис. 1.8, е). Виокремлюємо вузол 1 з епюри
− це реактивний момент у рухомому затисненні вузла 1 основної системи (рис. 1.4, б), від зовнішнього навантаження, тобто у вантажному стані (рис. 1.8, е). Виокремлюємо вузол 1 з епюри  ;
; .
. (рис. 1.8, в, г, д) і зовнішнього навантаження (рис 1.8, е).
(рис. 1.8, в, г, д) і зовнішнього навантаження (рис 1.8, е).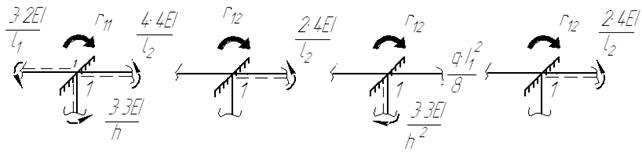
 ; б) визначення
; б) визначення  ; в) визначення
; в) визначення  ; г) визначення
; г) визначення 
 ; б) визначення
; б) визначення  ; в) визначення
; в) визначення  ; г) визначення
; г) визначення 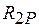
 (рис. 1.8, д), потрібно перемістити в напрямку цього невідомого додатковий опорний стержень разом із вузлами 1, 2, 3, які розташовані на одній горизонталі, внаслідок чого, зазнають перекосів вертикальні стержні рами. Отже, перетин повинен проходити саме через ці два вертикальні стержні й додатковий опорний стержень. Цей перетин зображено на рис. 1.8 (б).
(рис. 1.8, д), потрібно перемістити в напрямку цього невідомого додатковий опорний стержень разом із вузлами 1, 2, 3, які розташовані на одній горизонталі, внаслідок чого, зазнають перекосів вертикальні стержні рами. Отже, перетин повинен проходити саме через ці два вертикальні стержні й додатковий опорний стержень. Цей перетин зображено на рис. 1.8 (б).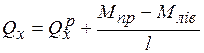 .
. – це реакція накладеного опорного стержня від одиничного кута повороту
– це реакція накладеного опорного стержня від одиничного кута повороту  , тобто в першому одиничному стані (рис. 1.8, в). Для його визначення перетином, показаним на рис. 1.8 (б), виокремлюємо фрагмент основної системи (рис. 1.12, а). До цього фрагмента прикладаємо шукану реакцію
, тобто в першому одиничному стані (рис. 1.8, в). Для його визначення перетином, показаним на рис. 1.8 (б), виокремлюємо фрагмент основної системи (рис. 1.12, а). До цього фрагмента прикладаємо шукану реакцію  та поперечні сили в стержнях, які перерізані перетином
та поперечні сили в стержнях, які перерізані перетином  (рис. 1.12, а), складаємо рівняння рівноваги:
(рис. 1.12, а), складаємо рівняння рівноваги: .
. – це реакція накладеного опорного стержня від одиничного кута повороту
– це реакція накладеного опорного стержня від одиничного кута повороту  , тобто в другому одиничному стані (рис. 1.8, г).
, тобто в другому одиничному стані (рис. 1.8, г). (рис. 1.12, б).
(рис. 1.12, б). ;
;  .
. – це реакція накладеного опорного стержня від поступального переміщення
– це реакція накладеного опорного стержня від поступального переміщення 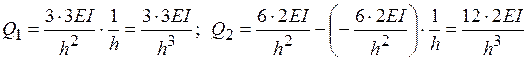 (рис. 1.12, в).
(рис. 1.12, в). .
. – це реакція накладеного опорного стержня основної системи від зовнішнього навантаження, тобто у вантажному стані (рис. 1.8, е). Знову відокремлюємо той самий фрагмент основної системи та прикладаємо шукану реакцію та поперечні сили в перерізаних стержнях
– це реакція накладеного опорного стержня основної системи від зовнішнього навантаження, тобто у вантажному стані (рис. 1.8, е). Знову відокремлюємо той самий фрагмент основної системи та прикладаємо шукану реакцію та поперечні сили в перерізаних стержнях 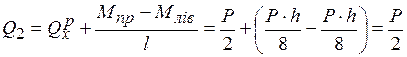 (рис. 1.12, г). Складаємо рівняння рівноваги:
(рис. 1.12, г). Складаємо рівняння рівноваги: .
.

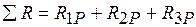
 .
.

 .
. на кожну одиничну
на кожну одиничну  , побудовану в основній системі, і в порівнянні одержаних результатів з сумами одиничних коефіцієнтів відповідного рядка матриці коефіцієнтів:
, побудовану в основній системі, і в порівнянні одержаних результатів з сумами одиничних коефіцієнтів відповідного рядка матриці коефіцієнтів: .
. .
. і в порівнянні одержаного результату з сумою всіх вантажних коефіцієнтів у відповідному стовпці матриці коефіцієнтів, але з протилежним знаком:
і в порівнянні одержаного результату з сумою всіх вантажних коефіцієнтів у відповідному стовпці матриці коефіцієнтів, але з протилежним знаком: .
.


