Сутність методу переміщень та визначення ступеня кінематичної невизначуваності системи
Метод переміщень являється одним із багатьох методів розрахунку статично невизначуваних систем, який був розроблений і впроваджений у практику пізніше за метод сил, але набув більшого поширення при «ручному» (без застосування комп’ютерних програм) розрахунку споруд, завдяки простоті та меншій трудомісткості обчислень для значної кількості досліджуваних об’єктів. Метод переміщень передбачає передусім обчислення певного набору переміщень, знання яких дає змогу визначити внутрішні зусилля й переміщення в будь-якому перерізі розрахункової системи. Визначимо, які переміщення прямолінійного стержня постійної жорсткості необхідно й достатньо знати, щоб визначити внутрішні зусилля в будь-якому його перерізі. Напружено-деформований стан стержневого елемента цілком визначається прикладеним до нього навантаженням і переміщеннями перерізів, в яких цей елемент приєднується до інших стержнів системи. Для таких стержнів, при будь-яких закріпленнях на кінцях, внутрішні зусилля й поперечні переміщення в усіх перерізах визначаються кутами повороту та відносними поступальними переміщеннями їхніх кінців, а також зовнішнім навантаженням на стержні. Тому в методі переміщень як основний елемент обирають саме прямолінійний стержень постійної жорсткості. Отже, якщо визначити кути повороту лівого ( У стержневих системах, кути між стержнями, які збігаються в жорсткому вузлі, повертаються на однаковий кут. Тому, за невідомі методу переміщення при розрахунку статично невизначуваних систем приймаються кути повороту жорстких вузлів системи та незалежні поступальні переміщення її вузлів . Ці невідомі методу переміщень позначаються літерами Кількість основних невідомих методу переміщень називається ступенем кінематичної невизначуваності системи (k). Її можна визначити за формулою:
де
Жорсткими вузлами є всі місця з’єднання кінців прямолінійних стержнів за допомогою припаювання. При підрахунку кількості жорстких вузлів системи не враховуються вузли, кутові переміщення яких відомі, наприклад, жорсткі опорні вузли. Для визначення кількості незалежних поступальних переміщень системи доцільно скористатись її шарнірною схемою. Шарнірна схема системи утворюється введенням наскрізних (повних) шарнірів у всі жорсткі вузли вихідної системи, включаючи й опорні вузли. Статично визначувані консолі можна відкидати. Геометрична змінність шарнірної системи визначена за формулою Чебишова дорівнює кількості незалежних поступальних переміщень вузлів вихідної системи.
де
Розглянемо кілька прикладів визначення ступеня кінематичної невизначуваності ( Для рами, що зображена на рис. 1.1(а), кількість кутових переміщень
а) геометрична схема рами; б) шарнірна схема рами Рисунок 1.1 – Геометрична та шарнірна схеми рами Для визначення кількості незалежних поступальних переміщень вузлів рами скористуємось її шарнірною схемою, яку отримаємо за допомогою введення наскрізних шарнірів у жорсткі вузли
Отже, для системи, що зображена на рис. 1.1 (а), маємо ступінь кінематичної невизначуваності
Для рами, що зображена на рис. 1.2 (а),кількість кутових переміщень
Кількість незалежних поступальних переміщень вузлів рами визначаємо як геометричну змінність шарнірної системи (рис. 1.2, б), яку отримали за допомогою введення наскрізних шарнірів у жорсткі вузли
а) геометрична схема; б) шарнірна схема Рисунок 1.2 – Статично невизначувана рама
Отже, для рами, що зображена на рис. 1.2 (а), ступінь кінематичної невизначуваності (
|
) та правого (
) кінця такого стержня, а також відносне переміщення їх (
), цього буде достатньо, щоб визначити внутрішні зусилля в будь-якому перерізі стержня. Саме ці переміщення (
(і = 1, 2, 3…).
,
− кількість кутових переміщень жорстких вузлів системи;
− кількість незалежних поступальних переміщень вузлів системи.
, або
,
− число дисків (стержнів) системи;
− число простих шарнірів;
− число опорних в’язей;
− число вузлів системи;
− число стержнів системи.
) системи, наприклад, рами (рис. 1.1).
і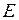 
.
,
.
.
:
.
.
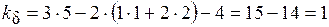