ПРИКЛАД РОЗРАХУНКУ СТАТИЧНО НЕВИЗНАЧУВАНОЇ РАМИ ЗА МЕТОДОМ ПЕРЕМІЩЕНЬ У КАНОНІЧНІЙ ФОРМІ
Схему рами та навантаження наведено на рис. 2.1.
Рисунок 2.1 – Розрахункова схема Для заданої рами потрібно: 1. Визначити ступінь кінематичної невизначуваності рами. 2. Створити основну та еквівалентну системи методу переміщень. 3. Скласти систему канонічних рівнянь для визначення основних невідомих переміщень. 4. Побудувати в основній системі епюри згинальних моментів в одиничних і вантажному станах. 5. Визначити коефіцієнти та вільні члени системи канонічних рівнянь статичним способом. Виконати їх перевірки. 6. Розв’язати систему канонічних рівнянь. 7. Побудувати парціальні епюри згинальних моментів. 8. Побудувати остаточну епюру дійсних згинальних моментів рами. 9. Виконати статичну та кінематичну перевірку остаточної епюри зги-нальних моментів. 10. Побудувати епюри поперечних та поздовжніх сил. 11. Визначити опорні реакції й виконати загальну перевірку умов рівноваги заданої рами. 12. Побудувати деформовану вісь рами.
2.1 Ступінь кінематичної невизначуваності рами
Ступінь кінематичної невизначуваності рами обчислюється за формулою:
де
де
Отже, для перетворення шарнірної системи в геометрично незмінювану систему достатньо закріпити вузли Ступінь кінематичної невизначуваності заданої рами
2.2 Основна система методу переміщень Розрахунок статично невизначуваної рами полягає в тому, що замість неї розглядається така створена з неї система (рис. 2.4), розрахунок якої можна здійснити за допомогою вже відомих засобів. Така нова система називається основною системою, вона дає можливість усунути переміщення всіх вузлів системи.
Рисунок 2.2 – Картина геометричної незмінності (перекосів) рами
Основну систему отримують із заданої шляхом накладання на всі вузли рами додаткових в’язей двох видів, які перешкоджають повороту жорстких вузлів та їх можливим лінійним переміщенням, за рахунок чого рама перетворюється в систему однопрогонових балок постійної жорсткості з нерухомими опорами, для розрахунку котрих є готові таблиці (додаток Б). Число в’язей, що вводяться в основну систему, дорівнює ступеню кінематичної невизначуваності системи, тобто трьом. Число додаткових «плаваючих» затиснень співпадає зі ступенем кутових переміщень Таким чином, основна система (рис. 2.4) перетворює вихідну розрахункову схему статично невизначеної рами в набір однопрогонових балок постійної жорсткості з нерухомими опорами, які не дають змоги кінцям балок мати кутові та поступальні переміщення.
2.3 Еквівалентна система
Вузли вихідної схеми рами (рис. 2.3) при зовнішньому навантаженні мають переміщення – кути повороту жорстких вузлів В і С та їх поступальні переміщення в горизонтальному напрямку. У створеній основній системі (рис. 2.4) ці переміщення вузлів виключені накладеними додатковими в’язями – «плаваючими» затисненнями та додатковим горизонтальним опорним стержнем. Для усунення цих відмін у деформаціях вихідної та основної систем надамо в основній системі додатковим в’язям поки що невідомі переміщення цих вузлів (рис. 2.5), тобто, жорсткий вузол В, разом з «плаваючим» затисненням (1), повернемо на кут, що дорівнює Таким чином, за невідомі приймаємо кути повороту жорстких вузлів рами Якщо ці переміщення вузлів (
2.4 Канонічні рівняння
У додаткових в’язях основної системи від навантаження виникають реактивні сили, яких немає у вихідній рамі, через відсутність цих додаткових в’язей. У «плаваючих» затисненнях жорстких вузлів виникають реактивні моменти, у додаткових опорних стержнях – реактивні сили, тобто реакції. Отже, необхідно скласти математичні умови реактивних сил накладених додаткових в’язей, які дорівнюють нулю. На підставі принципу суперпозиції сумарний реактивний момент у «плаваючому» затисненні першого вузла В від невідомих переміщень ( Канонічні рівняння методу переміщень встановлюють еквівалентність основної та заданої систем. Для заданої рами
Рисунок 2.3 – Розрахункова схема рами
Рисунок 2.4 – Основна система
Рисунок 2.5 – Еквівалентна система
Таким чином, фізичний зміст кожного з цих рівнянь полягає в тому, що сумарна реактивна сила у відповідній додатковій в’язі (реактивний момент у «плаваючому» затисненні, або реакція в додатковому опорному стержні) основної системи від усіх невідомих переміщень Ця сукупність залежностей є розв’язувальними рівняннями та називається системою канонічних рівнянь методу переміщень (2.2). Ці рівняння є рівняннями статичної рівноваги системи. Основними невідомими цих рівнянь являються переміщення, виключені додатковими в’язями, де Коефіцієнти при невідомих першого рядка системи канонічних рівнянь являють собою одиничний реактивний момент у «плаваючому» за-тисненні вузла В основної системи від дії одиничних невідомих переміщень Коефіцієнти при невідомих другого рядка канонічних рівнянь являють собою одиничний реактивний момент у «плаваючому» затисненні вузла С основної системи від дії одиничних невідомих переміщень Коефіцієнти при невідомих третього рядка канонічних рівнянь являють собою одиничну реакцію в додатковому опорному стержні основної системи від дії невідомих переміщень Вільні члени канонічних рівнянь являють собою вантажні реакції в додаткових в’язях основної системи від дії зовнішнього навантаження. Для визначення одиничних реакцій та вільних членів канонічних рівнянь необхідно мати епюри внутрішніх зусиль в основній системі методу переміщень в одиничних та вантажному станах.
2.5 Епюри зусиль в основній системі методу переміщень
Основна система методу переміщень являє собою набір однопрогонових балок постійної жорсткості з нерухомими опорами, які не дають кінцям балок мати кутові та поступальні переміщення. Для побудови епюр внутрішніх зусиль у цих балках, які є статично невизначуваними, необхідно заздалегідь визначити зусилля від дії різних зовнішніх навантажень, переміщень їхніх опор. Ці розрахунки виконуються різними способами побудови епюри згинальних моментів та поперечних сил від будь-якого навантаження. Результати розрахунків та епюри згинальних моментів однопрогонових статично невизначуваних балок при різних граничних умовах та деяких зовнішніх навантаженнях наведено в додатку Б. Одиничні та вантажні епюри для основної системи методу переміщень являють собою сукупність епюр згинальних моментів окремих балок, що складають цю систему, від переміщень їхніх опор, та від дії зовнішнього місцевого навантаження. Будуємо одиничну епюру згинальних моментів У додатку Б відшукуємо розрахункову схему аналогічної балки й за формулами визначаємо опорні реакції Стержень ВС являє собою балку з жорстким затисненням опор та змушеним поворотом затиснення опори В на одиничний кут Опори стержнів СЕ і СD не мають змушених переміщень, і ординати згинальних моментів нульові. Аналогічно будуємо одиничну епюру згинальних моментів Стержень CD примикає до вузла С і має на його опорі змушений кут повороту Стержень СЕ також примикає до вузла С і має на його опорі змушений кут повороту Опори стержня АВ не мають змушених переміщень, тому ординати згинальних моментів нульові. Будуємо одиничну епюру згинальних моментів Будуємо вантажну епюру згинальних моментів
2.6 Статичний спосіб визначення коефіцієнтів і вільних членів системи канонічних рівнянь та їх перевірка
Нагадаємо, що коефіцієнт, або вільний член системи канонічних рівнянь являє собою реактивну силу, що виникає у відповідній додатковій в’язі основної системи від одиничного значення невідомого переміщення 1. Реактивні моменти в рухомих «плаваючих» затисненнях. 2. Реакції в додаткових опорних стержнях. Для визначення реактивних моментів у «плаваючих» затисненнях виокремлюємо вузол основної системи разом із затисненням з епюри згинальних моментів відповідного одиничного або вантажного стану. До вузла прикладаємо невідомий реактивний момент із додатнім напрямом у рухомому затисненні, а також згинальні моменти в перерізах стержнів. Складаємо рівняння рівноваги цього виокремленого вузла Для заданої рами перший рядок коефіцієнтів системи канонічних рівнянь обчислюємо як реактивний момент у «плаваючому» затисненні 1 вузла В основної системи від одиничних невідомих переміщень Коефіцієнт
Коефіцієнт
Коефіцієнт
Вільний член Виокремлюємо вузол В з вантажної епюри
Другий рядок коефіцієнтів системи канонічних рівнянь обчислюємо як реактивний момент у рухомому затисненні 2 вузла С основної системи від одиничних невідомих переміщень Коефіцієнт
Рисунок 2.6 – Одинична епюра переміщень від одиничного навантаження
Рисунок 2.7 – Одинична епюра переміщень від одиничного навантаження
Рисунок 2.8 – Одинична епюра переміщень від одиничного навантаження
Рисунок 2.9 – Одинична епюра переміщень від постійного навантаження
Коефіцієнт
Коефіцієнт
Вільний член
Третій рядок коефіцієнтів системи канонічних рівнянь являють собою силові реакції в додатковому опорному стержні, введеному при створенні основної системи. Для обчислення їхньої величини необхідно розглянути умови рівноваги відокремленого перетином фрагмента основної системи (рис. 2.12). Перетин повинен проходити через додатковий стержень, в якому обчислюється реакція, а також через усі стержні основної системи які зазнають перекосів у напрямі цього додаткового стержня від примусового поступального переміщення До відокремленого фрагмента слід прикласти всі сили, що діють на нього, в тому числі, зусилля в перерізах стержнів. Поперечні сили в перерізах отримують з епюр згинальних моментів на цих стержнях, за формулою:
Шукана реакція в додатковому опорному стержні визначається з рівняння рівноваги у вигляді суми проекцій на вісь у напрямку додаткового стержня (рис. 2.13). Обчислюємо третій рядок коефіцієнтів системи канонічних рівнянь. Коефіцієнт До цього фрагмента прикладаємо шукану реакцію перерізаного опорного стержня
Реакцію
Коефіцієнт
Реакцію
Коефіцієнт
Реакцію
Вільний член До цього фрагмента прикладаємо шукану реакцію
Підставляємо визначені коефіцієнти в систему канонічних рівнянь і виконуємо перевірку їх значення.
Рисунок 2.10 – Визначення коефіцієнтів канонічних рівнянь
Перевірка правильності обчислення коефіцієнтів і вільних членів канонічних рівнянь. Для перевірки правильності обчислення коефіцієнтів будуємо сумарну одиничну епюру згинальних моментів
Порядкова перевірка одиничних коефіцієнтів кожного рядку канонічних рівнянь
Універсальна перевірка одиничних коефіцієнтів у всіх рядках канонічних рівнянь полягає в тому, що сума всіх одиничних коефіцієнтів у всіх рядках дорівнює результату перемноження сумарної одиничної епюри на ту ж сумарну одиничну епюру.
Постовпцева перевірка вантажних коефіцієнтів у всіх рядках канонічних рівнянь полягає в тому, що сума вантажних коефіцієнтів дорівнює по значенню, але з протилежним знаком результату переміщення сумарної одиничної епюри на вантажну епюру, побудовану в статично визначеній системі методу сил
а) перевірка 1; б) перевірка 2; в) перевірка 3; г) перевірка 4 Рисунок 2.12 – Перевірка коефіцієнтів і вільних членів канонічних рівнянь
Перевіримо коефіцієнти канонічних рівнянь для заданої рами, підставивши та розділивши їх значення на EI.
Порядкова перевірка
Рисунок 2.13 – Сумарна одинична епюра моментів
Рисунок 2.14 – Вантажна епюра моментів для статично визначеної системи
Універсальна перевірка
Постовпцева перевірка
2.7 Розв’язання системи канонічних рівнянь та визначення невідомих методу переміщень
Після перевірки підставимо визначені коефіцієнти та вільні члени в систему канонічних рівнянь, яка буде мати такий вигляд:
Розв’язуємо систему канонічних рівнянь відомими методами, наприклад, способом Гауса.
І.
ІІ.
ІІІ.
Таблиця 2.1 – Розв’язання системи канонічних рівнянь по методу Гауса
Перевіряємо правильність розв’язання системи канонічних рівнянь.
Розв’язавши систему канонічних рівнянь, отримали значення основних невідомих переміщень:
Таким чином, розкрита кінематична невизначуваність рами.
2.8 Визначення дійсних внутрішніх зусиль та побудова епюр внутрішніх зусиль M, Q, N
Отримавши значення й напрямок основних невідомих переміщень
Парціальні епюри Остаточна епюра згинальних моментів (
|


 , (2.1)
, (2.1) − кількість кутових переміщень жорстких вузлів. Рама має два жорсткі вузли – вузол В і вузол С.
− кількість кутових переміщень жорстких вузлів. Рама має два жорсткі вузли – вузол В і вузол С. .
. − кількість незалежних поступальних переміщень вузлів рами, що дорівнює геометричній змінності системи
− кількість незалежних поступальних переміщень вузлів рами, що дорівнює геометричній змінності системи  , яка утворюється із заданої шляхом введення в усі жорсткі вузли (включно з опорними) наскрізних (повних) шарнірів (рис. 2.2):
, яка утворюється із заданої шляхом введення в усі жорсткі вузли (включно з опорними) наскрізних (повних) шарнірів (рис. 2.2): ;
; ,
, – кількість простих дисків (стержнів);
– кількість простих дисків (стержнів); – кількість простих шарнірів;
– кількість простих шарнірів; – кількість опорних простих в’язей;
– кількість опорних простих в’язей; – кількість вузлів в’язей;
– кількість вузлів в’язей; – кількість стержнів рами.
– кількість стержнів рами. ;
; .
. і
і  .
.
 , а число додаткових стержнів – зі ступенем можливих лінійних переміщень вузлів
, а число додаткових стержнів – зі ступенем можливих лінійних переміщень вузлів  .
. , другий жорсткий вузол С, разом із рухомим затисненням (2), повернемо на кут
, другий жорсткий вузол С, разом із рухомим затисненням (2), повернемо на кут  , і надамо цим вузлам, разом з опорним вузлом Е і додатковим стержнем (3), переміщення в горизонтальному напрямі, на величину, що дорівнює
, і надамо цим вузлам, разом з опорним вузлом Е і додатковим стержнем (3), переміщення в горизонтальному напрямі, на величину, що дорівнює  , а також розмістимо задане зовнішнє навантаження (рис. 2.5).
, а також розмістимо задане зовнішнє навантаження (рис. 2.5). вони мають наступний вигляд:
вони мають наступний вигляд:



 і зовнішнього навантаження дорівнює нулю.
і зовнішнього навантаження дорівнює нулю. .
. (рис. 2.6) в першому одиничному стані основної системи, від одиничного значення невідомого кута
(рис. 2.6) в першому одиничному стані основної системи, від одиничного значення невідомого кута  повороту першого жорсткого вузла В з «плаваючим» затисненням. Спочатку потрібно з’ясувати, опори яких стержнів основної системи знаходяться у вузлі В, і на яку саме величину переміщуються. Стержень АВ являє собою балку з жорстким затисненням опор та змушеним поворотом затиснення на опорі В на одиничний кут
повороту першого жорсткого вузла В з «плаваючим» затисненням. Спочатку потрібно з’ясувати, опори яких стержнів основної системи знаходяться у вузлі В, і на яку саме величину переміщуються. Стержень АВ являє собою балку з жорстким затисненням опор та змушеним поворотом затиснення на опорі В на одиничний кут  .
. та опорні моменти на кінцях балок, і на стержні АВ будуємо одиничну епюру згинальних моментів
та опорні моменти на кінцях балок, і на стержні АВ будуємо одиничну епюру згинальних моментів  .
. .
. (рис. 2.7) у другому одиничному стані основної системи від дії одиничного значення невідомого кута повороту
(рис. 2.7) у другому одиничному стані основної системи від дії одиничного значення невідомого кута повороту  другого жорсткого вузла С з «плаваючим» затисненням. У вузлі С сходяться стержні ВС із змушеним кутом повороту опори С на кут
другого жорсткого вузла С з «плаваючим» затисненням. У вузлі С сходяться стержні ВС із змушеним кутом повороту опори С на кут  (рис. 2.8) у третьому одиничному стані від дії одиничного поступального переміщення додаткового опорного стержня в горизонтальному напрямку
(рис. 2.8) у третьому одиничному стані від дії одиничного поступального переміщення додаткового опорного стержня в горизонтальному напрямку  . Якщо переміщується опорний вузол Е разом із додатковим стержнем, то переміщується в горизонтальному напрямі й на таку ж величину жорсткі вузли В і С, у результаті чого отримує змушене одинарне
. Якщо переміщується опорний вузол Е разом із додатковим стержнем, то переміщується в горизонтальному напрямі й на таку ж величину жорсткі вузли В і С, у результаті чого отримує змушене одинарне  (рис. 2.9) у вантажному стані основної системи на тих стержнях, які несуть поперечне зовнішнє навантаження. За допомогою додатка Б будуємо вантажну епюру.
(рис. 2.9) у вантажному стані основної системи на тих стержнях, які несуть поперечне зовнішнє навантаження. За допомогою додатка Б будуємо вантажну епюру. і визначаємо шуканий коефіцієнт.
і визначаємо шуканий коефіцієнт. – це реактивний момент у рухомому затисненні 1, від одиничного кута повороту
– це реактивний момент у рухомому затисненні 1, від одиничного кута повороту  , тобто в першому одиничному стані. Виокремлюємо вузол В з епюри
, тобто в першому одиничному стані. Виокремлюємо вузол В з епюри  .
. – це реактивний момент у рухомому затисненні 1, від одиничного кута повороту
– це реактивний момент у рухомому затисненні 1, від одиничного кута повороту  , тобто в другому одиничному стані. Виокремлюємо вузол В (рис. 2.11) з епюри
, тобто в другому одиничному стані. Виокремлюємо вузол В (рис. 2.11) з епюри  .
. – це реактивний момент у рухомому затисненні 1, від одиничного поступального переміщення
– це реактивний момент у рухомому затисненні 1, від одиничного поступального переміщення  , тобто в третьому одиничному стані. Виокремлюємо вузол В (рис. 2.12) з епюри
, тобто в третьому одиничному стані. Виокремлюємо вузол В (рис. 2.12) з епюри  .
. – це реактивний момент у рухомому затисненні 1, від зовнішнього навантаження, тобто у вантажному стані.
– це реактивний момент у рухомому затисненні 1, від зовнішнього навантаження, тобто у вантажному стані.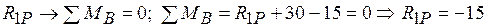 .
. і зовнішнього навантаження (рис. 2.11).
і зовнішнього навантаження (рис. 2.11). – це реактивний момент у рухомому затисненні 2, від одиничного кута повороту
– це реактивний момент у рухомому затисненні 2, від одиничного кута повороту  .
.



 – це реактивний момент у рухомому затисненні 2, від одиничного кута повороту
– це реактивний момент у рухомому затисненні 2, від одиничного кута повороту  .
. – це реактивний момент у рухомому затисненні 2, від одиничного поступального переміщення
– це реактивний момент у рухомому затисненні 2, від одиничного поступального переміщення  .
.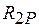 – це реактивний момент у другому затисненні 2, від зовнішнього навантаження, тобто у вантажному стані. Виокремлюємо вузол С з вантажної епюри
– це реактивний момент у другому затисненні 2, від зовнішнього навантаження, тобто у вантажному стані. Виокремлюємо вузол С з вантажної епюри  .
. .
. – це реакція накладеного опорного стержня 3 від одиничного кута повороту
– це реакція накладеного опорного стержня 3 від одиничного кута повороту  .
. .
. – це реакція накладеного опорного стержня 3 від одиничного кута повороту
– це реакція накладеного опорного стержня 3 від одиничного кута повороту  .
. визначаємо з рівнянь рівноваги фрагмента:
визначаємо з рівнянь рівноваги фрагмента: .
. – це реакція накладеного опорного стержня від одиничного поступального переміщення
– це реакція накладеного опорного стержня від одиничного поступального переміщення  , тобто в третьому одиничному стані. Для його визначення виокремлюємо той самий фрагмент у третьому одиничному стані основної системи (рис. 2.8). До цього фрагмента прикладаємо шукану реакцію
, тобто в третьому одиничному стані. Для його визначення виокремлюємо той самий фрагмент у третьому одиничному стані основної системи (рис. 2.8). До цього фрагмента прикладаємо шукану реакцію  .
. .
. – це реакція накладеного опорного стержня основної системи від зовнішнього навантаження, тобто у вантажному стані. Для цього виокремлюємо фрагмент основної системи (рис 2.9) у вантажному стані.
– це реакція накладеного опорного стержня основної системи від зовнішнього навантаження, тобто у вантажному стані. Для цього виокремлюємо фрагмент основної системи (рис 2.9) у вантажному стані. ;
;  .
.
 Рисунок 2.11 – Визначення коефіцієнтів канонічних рівнянь
Рисунок 2.11 – Визначення коефіцієнтів канонічних рівнянь від одночасної дії всіх основних невідомих, які дорівнюють одиниці. Епюру
від одночасної дії всіх основних невідомих, які дорівнюють одиниці. Епюру  .
. полягає в тому, що сума одиничних коефіцієнтів «
полягає в тому, що сума одиничних коефіцієнтів « » рядку дорівнює результату перемноження сумарної одиничної епюри на одиничну епюру
» рядку дорівнює результату перемноження сумарної одиничної епюри на одиничну епюру  :
: .
. .
. , яку отримують із заданої розрахункової схеми відкиданням зайвих в’язей, у тому числі обов’язково й тих в’язей, реакції в яких відшукуються:
, яку отримують із заданої розрахункової схеми відкиданням зайвих в’язей, у тому числі обов’язково й тих в’язей, реакції в яких відшукуються: .
.






 .
.





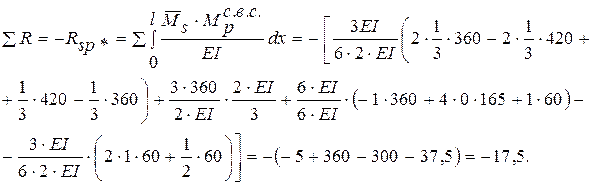
 ;
; ;
;
 ;
; ;
; .
. ;
;  ;
; 

 .
.
 .
. ;
;  .
.





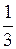
















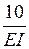






 ;
; ;
; .
. ;
;  ;
;  .
. (рис 2.15) та епюри згинальних моментів від зовнішнього навантаження в основній системі методу переміщень (рис. 2.9):
(рис 2.15) та епюри згинальних моментів від зовнішнього навантаження в основній системі методу переміщень (рис. 2.9): .
. наведені на рис. 2.15. Для їхнього отримання одиничні епюри згинальних моментів, які побудовані в основній системі методу переміщень (рис 2.6, 2.7, 2.8) домножуються на величину відповідних переміщень з урахуванням їх знаків.
наведені на рис. 2.15. Для їхнього отримання одиничні епюри згинальних моментів, які побудовані в основній системі методу переміщень (рис 2.6, 2.7, 2.8) домножуються на величину відповідних переміщень з урахуванням їх знаків. ) для заданої системи (рис 2.16) побудована як сума парціальної й вантажної епюр.
) для заданої системи (рис 2.16) побудована як сума парціальної й вантажної епюр.


