Окружность
Уравнение (х —a)2+ (у —b)2 = R 2 (1) определяет окружность радиуса R с центром С (a; b). Если центр окружности совпадает с началом координат, т.е. если a = 0, b = 0, то уравнение (1) принимает вид х 2 + у 2 = R 2 (2). Решить задачи: 2.42. Составить уравнение окружности в каждом из следующих случаев: 1) центр окружности совпадает с началом координат и её радиус R = 3; 2) центр окружности совпадает с точкой С (2; — 3) и её радиус R = 7; 3) окружность проходит через начало координат и её центр совпадает с точкой С (6; — 8); 4) окружность проходит через точку А (2; 6) и её центр совпадает с точкой С (—1; 2); 5) точки А (3; 2) и В (—1; 6) являются концами одного из диаметров окружности; 6) центр окружности совпадает с началом координат и прямая 3 х — 4 у + 20 = 0 является касательной к окружности; 7) центр окружности совпадает с точкой С (1; —1) и прямая 5 х —12 у + 9 = 0 является касательной к окружности; 8) окружность проходит через точки А (3; 1) и В (—1; 3), а её центр лежит на прямой 3 х — у — 2 = 0; 9) окружность проходит через три точки: А (1; 1), B (1; — 1) и С (2; 0); 10) окружность проходит через три точки: M 1(— 1; 5), М 2(— 2; — 2) и M 3 (5; 5). 2.43. Точка С (3; — 1) является центром окружности, отсекающей на прямой 2 х — 5 у + 18 = 0 хорду, длина которой равна 6. Составить уравнение этой окружности. 2.44. Написать уравнения окружностей радиуса R = х — 2 у — 1=0 в точке М 1 (3; 1). 2.45. Составить уравнение окружности, касающейся двух параллельных прямых: 2 х + у — 5 = 0, 2 х + у +15 = 0, причём одной из них — в точке А (2; 1). 2.46. Составить уравнения окружностей, которые проходят через точку А (1; 0) и касаются двух параллельных прямых: 2 х + у + 2 = 0, 2 х + у — 18 = 0. 2.47. Составить уравнение окружности, которая, имея центр на прямой 2 х + у = 0, касается прямых 4 х — 3 у +10 = 0, 4 х — 3 у — 30 = 0. 2.48. Составить уравнения окружностей, касающихся двух пересекающихся 2.49. Составить уравнения окружностей, проходящих через начало координат и касающихся двух пересекающихся прямых: х + 2 у – 9 = 0, 2 х – у + 2 = 0. 2.50. Составить уравнения окружностей, которые, имея центры на прямой 4 х – 5 у – 3 = 0, касаются прямых 2 х – 3 у – 10 = 0, 3 х – 2 у + 5 = 0. 2.51. Написать уравнения окружностей, проходящих через точку А (–1; 5) и касающихся двух пересекающихся прямых: 2.52. Написать уравнения окружностей, касающихся трёх прямых: 4 х – 3 у – 10 = 0, 3 х – 4 у – 5 = 0 и 3 х – 4 у – 15 = 0. 2.53. Написать уравнения окружностей, касающихся трёх прямых: 3 х + 4 у – 35 = 0, 3 х – 4 у – 35 = 0 и х – 1 = 0. 2.54. Какие из нижеприводимых уравнений определяют окружности? Найти центр С и радиус R каждой из них: 1) (х – 5)2 + (у + 2)2 = 25; 2) (х + 2)2 + у 2 = 64; 3) (х —5)2 + (у + 2)2 = 0; 4) х 2 + (у – 5)2 = 5; 5) х 2+ у 2 – 2 х + 4 у – 20 = 0; 6) х 2+ у 2 – 2 х + 4 у + 14 = 0; 7) х 2 + у 2 + 4 х – 2 у + 5 = 0; 8) х 2 + у 2 + х = 0, 9) х 2 + у 2 + 6 х – 4 у + 14 = 0; 10) х 2 + у 2 + у =0 2.55. Установить, какие линии определяются следующими уравнениями: 1) 2) 3) 4) 5) Изобразить эти линии на чертеже. Эллипс Основные теоретические сведения. Эллипс – геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная (большая, чем расстояние между фокусами).
F1(-c,0), F2(c,0) – фокусы;
Решить задачи: 2.56. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, кроме того, что: 1) его полуоси равны 5 и 2; 2) его большая ось равна 10, а расстояние между фокусами 2с = 8; 3) его малая ось равна 24, а расстояние между фокусами 2с =10; 4) расстояние между его фокусами 2с = 6 и эксцентриситет 5) его большая ось равна 20, а эксцентриситет 6) его малая ось равна 10, а эксцентриситет 7) расстояние между его директрисами равно 5 и расстояние между фокусами 2с = 4; 8) его большая ось равна 8, а расстояние между директрисами равно 16; 9) его малая ось равна 6, а расстояние между директрисами равно 13; 10) расстояние между его директрисами равно 32 и 2.57. Составить уравнение эллипса, фокусы которого лежат на оси ординат, симметрично относительно начала координат, зная, кроме того, что: 1) его полуоси равны соответственно 7 и 2; 2) его большая ось равна 10, а расстояние между фокусами 2с = 8; 3) расстояние между его фокусами 2с = 24 и эксцентриситет 4) его малая ось равна 16, а эксцентриситет 5) расстояние между его фокусами 2с = 6 и расстояние между директрисами равно 16 6) расстояние между его директрисами равно 2.58. Определить полуоси каждого из следующих эллипсов: 1) 4) х 2 + 5 y 2 = 15; 5) 4 х 2 + 9 у 2 = 25; 6) 9х2 + 25у2 = 1; 7) х 2 + 4 у 2 = 1; 8) 16 х 2 + у 2 = 16; 9) 25х2 + 9у2 = 1; 10) 9 х 2 + у 2 = 1. 2.59. Дан эллипс 9х2 + 25у2 = 225. Найти: 1) его полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис. 2.60. Вычислить площадь четырёхугольника, две вершины которого лежат в фокусах эллипса х 2 + 5 у 2 = 20, а две другие совпадают с концами его малой оси. 2.61. Дан эллипс 9 х 2 + 5 у 2 = 45. Найти: 1) его полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис. 2.62. Вычислить площадь четырёхугольника, две вершины которого лежат в фокусах эллипса 9 х 2 + 5 у 2 = 1, две другие совпадают с концами его малой оси. 2.63. Вычислить расстояние от фокуса F (c; 0) эллипса
до односторонней с этим фокусом директрисы. 2.64. Определить, какие из точек A 1(—2; 3), А 2(2; —2), А 3 (2; —4), А 4(—1; 3), А 5(—4; —3), А 6(3; —1), А 7(3; —2), А 8 (2; 1), А 9(0; 15) и А 10(0; —16) лежат на эллипсе 8х2+5у2 = 77, какие внутри и какие вне его. 2.65. Установить, какие линии определяются следующими уравнениями: 1) 3) Изобразить эти линии на чертеже. 2.66. Эксцентриситет эллипса 2.67. Эксцентриситет эллипса 2.68. Дана точка М1 (2; 2.69. Убедившись, что точка М1 (— 4; 2,4) лежит на эллипсе 2.70. Эксцентриситет эллипса 2.71. Эксцентриситет эллипса 2.72. Определить точки эллипса до правого фокуса равно 14. 2.73. Определить точки эллипса до левого фокуса равно 2,5. 2.74. Через фокус эллипса к его большой оси. Определить расстояния от точек пересечения этого перпендикуляра с эллипсом до фокусов. 2.75. Составить уравнение эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно начала координат, если даны: 1) точка М1 (—2 2) точка M2 (2;—2) эллипса и его большая полуось а = 4; 3) точки M1(4;_— 4) точка M1 ( 5) точка М1 (2; — 6) точка M1 (8; 12) эллипса и расстояние r1 = 20 от неё до левого фокуса; 7) точка M1 (— 2.76. Определить эксцентриситет e эллипса, если: 1) его малая ось видна из фокусов под углом в 60°; 2) отрезок между фокусами виден из вершин малой оси под прямым углом; 3) расстояние между директрисами в три раза больше расстояния между фокусами; 4) отрезок перпендикуляра, опущенного из центра эллипса на его директрису, делится вершиной эллипса пополам. 2.77. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет и уравнения директрис: 1) 5х2 + 9у2 — 30х + 18у + 9 = 0; 2) 16х2 + 25у2 + 32х — 100у — 284 = 0; 3) 4х2 + 3у2 — 8х + 12у —32 = 0. 2.78. Установить, какие линии определяются следующими уравнениями: 1) 3) Изобразить эти линии на чертеже.
|

 , касающихся прямой
, касающихся прямой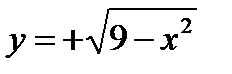 ; 6)
; 6)  ;
; ; 7)
; 7)  ;
; ; 8)
; 8)  ;
;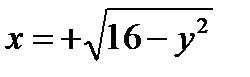 ; 9)
; 9)  ;
; ; 10)
; 10)  .
.
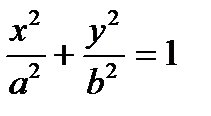 каноническое уравнение эллипса;
каноническое уравнение эллипса;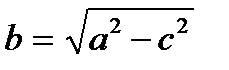 ;
; - эксцентриситет (ε<1);
- эксцентриситет (ε<1);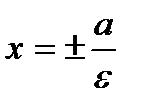 - уравнения директрис.
- уравнения директрис. ;
; ;
; ;
; .
.
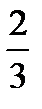
 и эксцентриситет
и эксцентриситет 
 ; 2)
; 2)  ; 3) х 2 + 25 у 2 = 25;
; 3) х 2 + 25 у 2 = 25;
 ; 2)
; 2)  ;
; ; 4)
; 4)  .
. , фокальный радиус точки М эллипса равен 10. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.
, фокальный радиус точки М эллипса равен 10. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы. , расстояние от точки М эллипса до директрисы равно 20. Вычислить расстояние от точки М до фокуса, одностороннего с этой директрисой.
, расстояние от точки М эллипса до директрисы равно 20. Вычислить расстояние от точки М до фокуса, одностороннего с этой директрисой.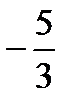 ) на эллипсе
) на эллипсе  составить уравнения прямых, на которых лежат фокальные радиусы точки M1.
составить уравнения прямых, на которых лежат фокальные радиусы точки M1. определить фокальные радиусы точки М1.
определить фокальные радиусы точки М1. , центр его совпадает с началом координат, один из фокусов F(—2; 0). Вычислить расстояние от точки M1 эллипса с абсциссой, равной 2, до директрисы, односторонней с данным фокусом.
, центр его совпадает с началом координат, один из фокусов F(—2; 0). Вычислить расстояние от точки M1 эллипса с абсциссой, равной 2, до директрисы, односторонней с данным фокусом. , центр его совпадает с началом координат, одна из директрис дана уравнением х =16. Вычислить расстояние от точки M1 эллипса с абсциссой, равной - 4, до фокуса, одностороннего с данной директрисой.
, центр его совпадает с началом координат, одна из директрис дана уравнением х =16. Вычислить расстояние от точки M1 эллипса с абсциссой, равной - 4, до фокуса, одностороннего с данной директрисой. , расстояние которых
, расстояние которых , расстояние которых
, расстояние которых проведён перпендикуляр
проведён перпендикуляр ) и М2(2
) и М2(2 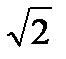 ; 3) эллипса;
; 3) эллипса; ; —1) эллипса и расстояние между его фокусами 2с =8;
; —1) эллипса и расстояние между его фокусами 2с =8; эллипса и его эксцентриситет
эллипса и его эксцентриситет  ;
;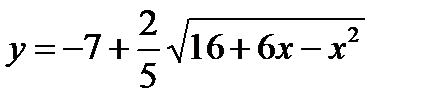 ; 2)
; 2)  ;
; ; 4)
; 4) 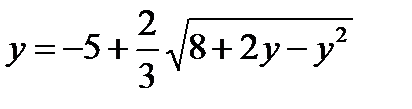 .
.


