1)  ;
;
2) 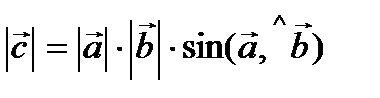 ;
;
3) Если  , то
, то 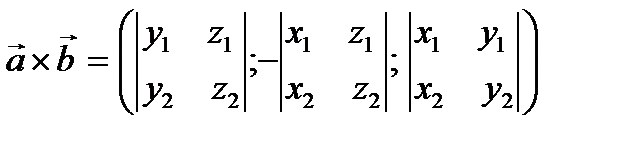
или 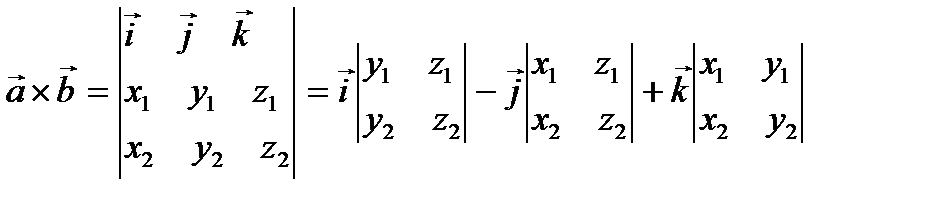 ,
,
где 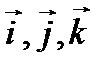 - единичные векторы на осях ОХ, ОY, OZ.
- единичные векторы на осях ОХ, ОY, OZ.
Свойства и приложения векторного произведения векторов:
1) 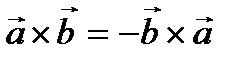 ;
;
2) 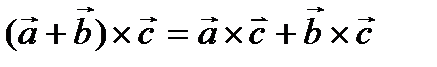 ;
;
3)  ;
;
4) 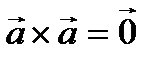 ;
;
5) 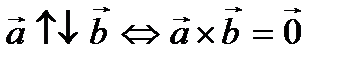 ;
;
6) 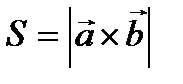 - площадь параллелограмма, построенного на векторах
- площадь параллелограмма, построенного на векторах 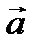 и
и 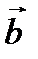 .
.
7) 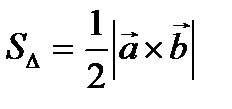 - площадь треугольника, построенного на векторах
- площадь треугольника, построенного на векторах 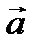
Пример 14.1. Вычислить площадь треугольника 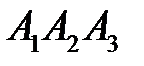 , если
, если
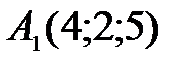 ;
;  ;
;  .
.
Решение: Площадь треугольника 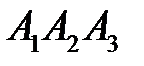 вычислим по формуле:
вычислим по формуле: 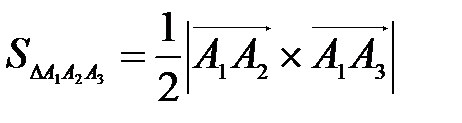 .
.
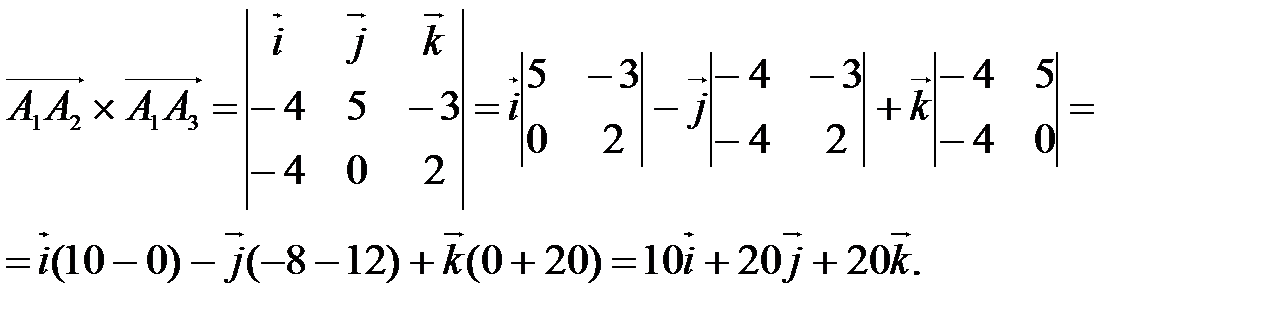
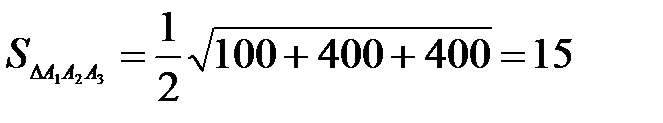 .
.
Ответ: 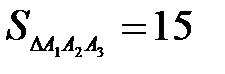 .
.
Пример 14.2. Дано разложение векторов  и
и  по векторам
по векторам  и
и  .
.
Найти площадь параллелограмма, построенного на векторах  и
и  .
.
 ,
,  ,
,  ,
,  ,
,  .
.
Решение:
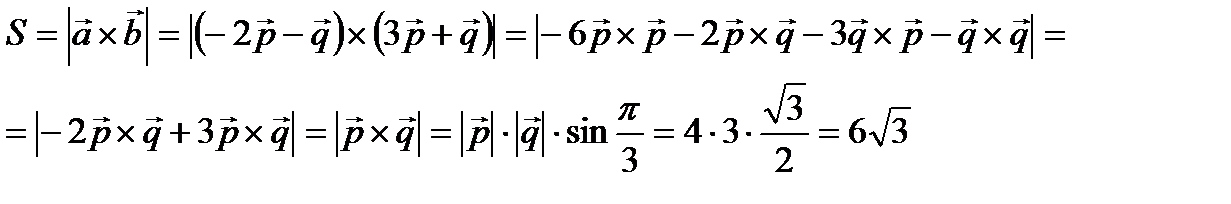
Ответ: 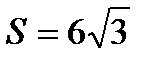 .
.
Решить задачи:
27. Найти векторное произведение векторов  и
и  , если А(2;3;0), B(1;-1;2), C(1;-1;0) и D(1;1;1);
, если А(2;3;0), B(1;-1;2), C(1;-1;0) и D(1;1;1);
28. Найти векторное произведение векторов  и
и  , если А(2;-1;1), B(0;-1;2), C(2;-1;0) и D(2;1;-1);
, если А(2;-1;1), B(0;-1;2), C(2;-1;0) и D(2;1;-1);
29. Найти площадь треугольника ABC с вершинами в точках А(1;1;-1), B(0;-1;2), C(2;-1;0);
30. Векторы 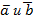 образуют угол
образуют угол  =
= 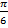 ; зная, что |
; зная, что |  | = 6, |
| = 6, | 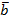 | = 5, вычислить |
| = 5, вычислить | 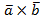 |; наибольшая площадь параллелограмма построенного на векторах
|; наибольшая площадь параллелограмма построенного на векторах 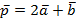 и
и 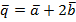 ; и синус угла между диагоналями параллелограмма построенного на векторах
; и синус угла между диагоналями параллелограмма построенного на векторах  и
и  .
.
31. Даны: |  | = 3, |
| = 3, | 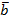 | = 26 и |
| = 26 и | 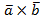 | = 72. Вычислить
| = 72. Вычислить 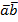 .
.
32. Даны точки А (1; 2; 0), В (3; 0; -3) и С (5; 2; 6). Вычислить площадь треугольника АВС.
33. Какому условию должны удовлетворять векторы 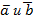 , что бы векторы
, что бы векторы 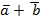 и
и 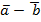 были коллинеарны?
были коллинеарны?
34. Сила 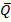 = {3; 4; -2} приложена к точке С (2; -1; 2). Определить величину и направляющие косинусы момента этой силы относительно начала координат.
= {3; 4; -2} приложена к точке С (2; -1; 2). Определить величину и направляющие косинусы момента этой силы относительно начала координат.
35. Даны вершины треугольника А (1; -1; 2), В (5; -6; 2) и С (1; 3; -1). Вычислить его высоты, опущенной из вершины В на сторону АС.
36. Векторы 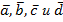 связанны соотношениями
связанны соотношениями 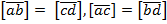 . Доказать коллинеарность векторов
. Доказать коллинеарность векторов 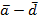 и
и 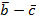 .
.
37.. Даны векторы  = {3; -1; -2} и
= {3; -1; -2} и 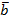 = {1; 2; -1}. Найти координаты векторного произведения (2
= {1; 2; -1}. Найти координаты векторного произведения (2 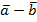 )
) 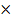 (2
(2 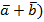 .
.
38. Даны векторы  = {2; -3; 1},
= {2; -3; 1}, 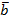 = {-3; 1; 2} и
= {-3; 1; 2} и  = {1; 2; 3}. Вычислить
= {1; 2; 3}. Вычислить  .
.

 ;
;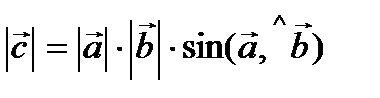 ;
; , то
, то 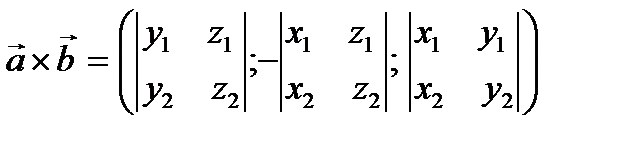
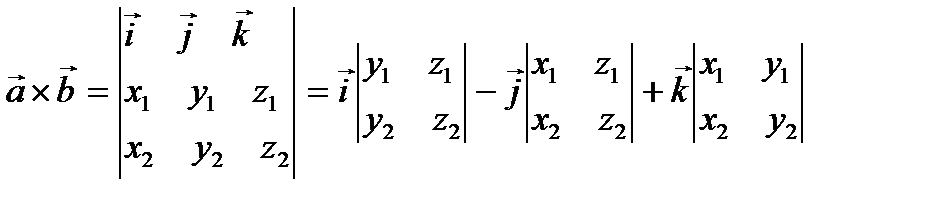 ,
,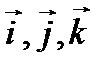 - единичные векторы на осях ОХ, ОY, OZ.
- единичные векторы на осях ОХ, ОY, OZ.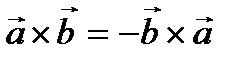 ;
;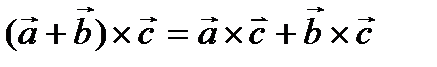 ;
; ;
;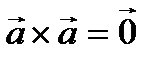 ;
;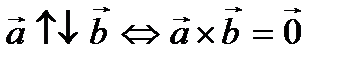 ;
;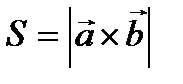 - площадь параллелограмма, построенного на векторах
- площадь параллелограмма, построенного на векторах 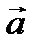 и
и 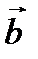 .
.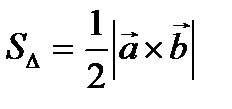 - площадь треугольника, построенного на векторах
- площадь треугольника, построенного на векторах 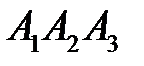 , если
, если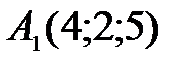 ;
;  ;
;  .
.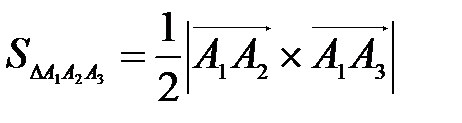 .
.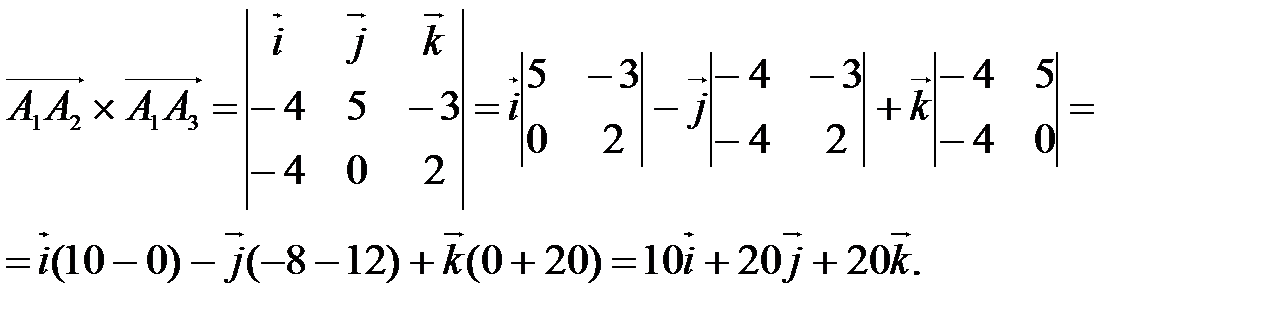
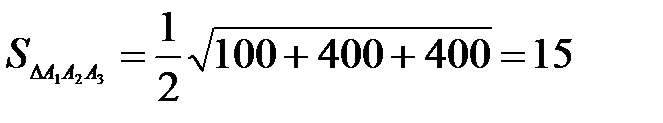 .
.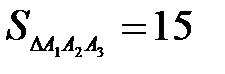 .
. и
и  по векторам
по векторам  и
и  .
. ,
,  ,
,  ,
,  ,
,  .
.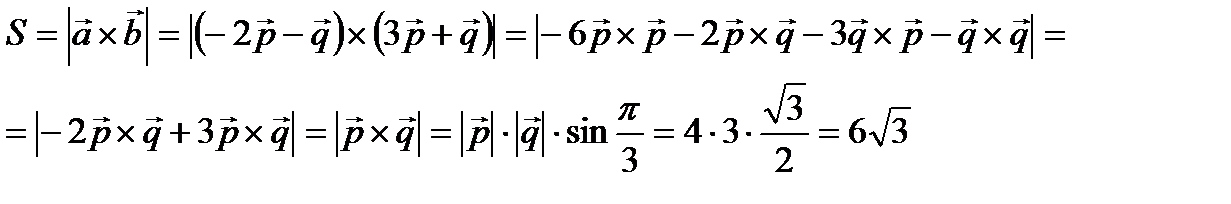
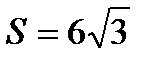 .
. и
и  , если А(2;3;0), B(1;-1;2), C(1;-1;0) и D(1;1;1);
, если А(2;3;0), B(1;-1;2), C(1;-1;0) и D(1;1;1);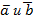 образуют угол
образуют угол  =
= 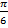 ; зная, что |
; зная, что |  | = 6, |
| = 6, | 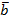 | = 5, вычислить |
| = 5, вычислить | 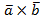 |; наибольшая площадь параллелограмма построенного на векторах
|; наибольшая площадь параллелограмма построенного на векторах 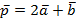 и
и 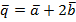 ; и синус угла между диагоналями параллелограмма построенного на векторах
; и синус угла между диагоналями параллелограмма построенного на векторах  и
и  .
.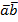 .
.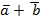 и
и 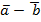 были коллинеарны?
были коллинеарны?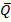 = {3; 4; -2} приложена к точке С (2; -1; 2). Определить величину и направляющие косинусы момента этой силы относительно начала координат.
= {3; 4; -2} приложена к точке С (2; -1; 2). Определить величину и направляющие косинусы момента этой силы относительно начала координат.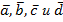 связанны соотношениями
связанны соотношениями 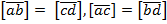 . Доказать коллинеарность векторов
. Доказать коллинеарность векторов 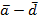 и
и 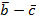 .
. = {3; -1; -2} и
= {3; -1; -2} и 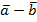 )
)  (2
(2 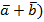 .
. = {1; 2; 3}. Вычислить
= {1; 2; 3}. Вычислить  .
.


