Операции над векторами
Разложение произвольного вектора по трем некомпланарным векторам. Операции над координатами векторов. Угол между векторами. Проекция вектора на ось. Если 1) 2) 3) 4) Если заданы две точки A(x1, y1, z1), B(x2, y2, z2), то 1) 2) если
В частности, если С – середина отрезка, то
Пример №12.1. По координатам вершин треугольника найти длины сторон Решение: Длины сторон Найдем координаты векторов
Длины векторов найдем по формуле:
Ответ: Пример № 12.2. Найдем разложение вектора
Решим систему методом Гаусса. Первое и третье уравнения системы оставляем без изменения, для получения второго уравнения умножим первое на 2 и сложим со вторым:
Первых два уравнения оставим без изменения, а для получения третьего умножим второе на -2 и сложим с третьим:
Таким образом, Ответ: Решить задачи: 1. Вычислить модуль вектора 2. Даны две координаты вектора 3. Определить начало вектора 4. Вычислить направляющие косинусы вектора 5. Вектор составляет осями ох и оz углы 6. По данным векторам 7. Даны: | 8. Даны два вектора 9. Даны три вершины параллелограмма ABCD: 10. Даны точки A (-1; 5; -10), В (5; 7; 8), С(2; 2; -7) и D (5; -4; 2). Проверить, что векторы 11. Найти орт вектора 12. На плоскости даны два вектора 13. Даны три вектора 14. Даны четыре вектора
|

 , то
, то - длина вектора;
- длина вектора; ;
; , k - число;
, k - число; .
.
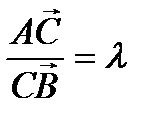 , тогда координаты точки С, делящей отрезок в заданном отношении, находятся по формулам:
, тогда координаты точки С, делящей отрезок в заданном отношении, находятся по формулам:
 .
.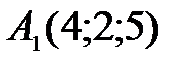 ;
;  ;
; 
 и
и  .
.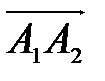 и
и  .
. ;
; ,
, 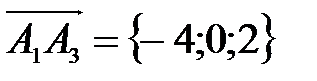 .
.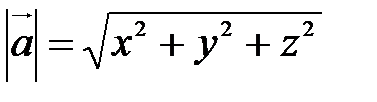 .
. ,
,  .
. ;
;  .
. по базису трех векторов
по базису трех векторов  ,
,  и
и 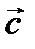 , то есть
, то есть  , где
, где  - неизвестные величины, для нахождения этих величин составим систему уравнений:
- неизвестные величины, для нахождения этих величин составим систему уравнений: , из условия
, из условия  .
.




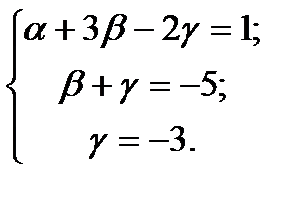
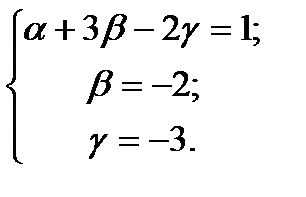

 .
. .
.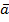 = {6; 3; -2}.
= {6; 3; -2}. ,
,  .Определить его третью координату
.Определить его третью координату  при условии, что |
при условии, что | 
 Какой угол он составляет с осью
Какой угол он составляет с осью  ?
?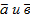 построить каждый из следующих векторов: 3) 2
построить каждый из следующих векторов: 3) 2  +
+  4)
4)  .
.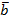 | = 19 и |
| = 19 и |  | = 24. Вычислить |
| = 24. Вычислить |  |.
|. .
.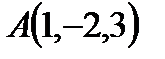 ,
,  ,
,  . Найдите вершину D.
. Найдите вершину D. коллинеарны, установить, какой из них длиннее другого и во сколько раз, как они направлены в одну или противоположные стороны.
коллинеарны, установить, какой из них длиннее другого и во сколько раз, как они направлены в одну или противоположные стороны. = {2; 3} и
= {2; 3} и  = {1; 2}. Найти разложение вектора
= {1; 2}. Найти разложение вектора  = {2; 1; -3}. Найти разложение вектора
= {2; 1; -3}. Найти разложение вектора  = {11; -6; 5} по базису
= {11; -6; 5} по базису  = {3; 7; -7}. Определить разложение вектора
= {3; 7; -7}. Определить разложение вектора 



