Практическое занятие 5
Матрицы, операции над матрицами Сложение матриц. Суммой двух матриц
Пример 5.1.
Отметим, что разность двух матриц определяется аналогично.
Умножение на число. Произведением матрицы Пример 5.2. . Пусть Пример 5.3. Заданы матрицы А= Решение:
Решить задачи: 1.83. Заданы матрицы А= 1.84. Заданы матрицы А= 1.85. Заданы матрицы А= 1.86. Заданы матрицы А= 1.87. Заданы матрицы А= 1.88. Заданы матрицы А= 1.89. Найдите 3A + 2B - 4C, Умножение матриц Произведением матрицы
Пример 5.4. Найдите произведение матриц: Решение:
Решить задачи: 1.90. Заданы матрицы А= 1.91. Заданы матрицы А= 1.92. Заданы матрицы А= 1.93. Заданы матрицы А= 1.94. Заданы матрицы А= 1.95. Заданы матрицы А= 1.96. Найдите произведение матриц ААТ: 1.97. Найдите произведение матриц АТА: 1.98. Найдите значение матричного многочлена f(A): Практическое занятие 6 Обратная матрица.
|

 и
и  называется матрица
называется матрица  такая, что
такая, что  .
.
 на число k называется матрица
на число k называется матрица  такая, что
такая, что  ,
, 
 и k =2, тогда
и k =2, тогда  .
.  и В=
и В=  . Сумма 5А-4В
. Сумма 5А-4В  равна…
равна…  ,
,  ,
, 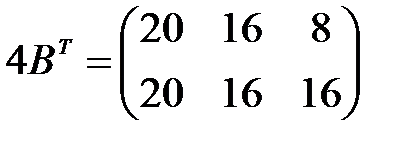 ,
, 
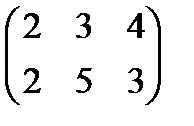 и В=
и В=  . Сумма 4А
. Сумма 4А  +5В равна
+5В равна и В=
и В=  . Сумма 6А
. Сумма 6А  и В=
и В=  . Сумма 2А+3В
. Сумма 2А+3В  и В=
и В=  . Сумма 6А-3В
. Сумма 6А-3В  и В=
и В=  . Сумма 3А
. Сумма 3А  и В=
и В= 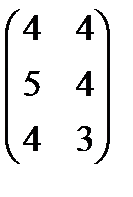 . Сумма 2А -3В
. Сумма 2А -3В 
 на матрицу
на матрицу  называется матрица
называется матрица  такая, что
такая, что  , где
, где 
 , т.е. элемент
, т.е. элемент  –й строки и
–й строки и  –го столбца
–го столбца .
.
 .
. .
. и В=
и В=  . Найдите произведение АВ
. Найдите произведение АВ и В=
и В=  . Найдите произведение АВ
. Найдите произведение АВ и В=
и В=  . Найдите произведение АВ
. Найдите произведение АВ 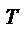
 и В=
и В=  . Найдите произведение ВА
. Найдите произведение ВА и В=
и В= 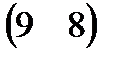 . Произведением ВА является…
. Произведением ВА является… и В=
и В= 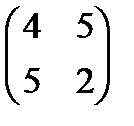 . Произведением АВ является
. Произведением АВ является .
. .
. .
.


