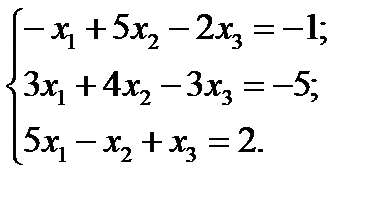Решение систем линейных уравнений методом Жордана-Гаусса
Пример 1. Решить систему методом Жордана-Гаусса
Решение:
Записываем полученные данные в таблицу. Осуществляем контроль:
Т.к. элементы контрольного столбца, вычисленные по правилу прямоугольника, равны элементам контрольного столбца, вычисленные суммированием элементов по строке, то полученная таблица составлена верно. Выбранному разрешающему элементу соответствовала переменная Переходим к следующему шагу. 2-й шаг. Выбираем разрешающий элемент
Третий столбец в новую таблицу можно переписать без изменений, т.к. в разрешающей стоке в третьем столбце стоит ноль. Записываем полученные данные в таблицу. Осуществляем контроль:
Т.к. элементы контрольного столбца, вычисленные по правилу прямоугольника, равны элементам контрольного столбца, вычисленные суммированием элементов по строке, то полученная таблица составлена верно. Выбранному разрешающему элементу соответствовала переменная Переходим к следующему шагу. 3-й шаг. Выбираем разрешающий элемент из третьей строчки, т.к. в этой третьей строке только один элемент отличный от нуля, то в качестве разрешающего элемента выбираем этот элемент
Первый, третий и контрольный столбцы в новую таблицу можно переписать без изменений, т.к. в разрешающей строке в первом, третьем и контрольном столбцах стоят нули. Записываем полученные данные в таблицу. Осуществляем контроль:
Т.к. элементы контрольного столбца, вычисленные по правилу прямоугольника, равны элементам контрольного столбца, вычисленные суммированием элементов по строке, то полученная таблица составлена верно. Выбранному разрешающему элементу соответствовала переменная Т.к. все строки побывали разрешающими и система приведена к единичному базису, то выписываем ответ:
Ответ: Задание 1.117. Решить систему линейных уравнений методом Жордана – Гаусса. 1) 3) 5)
|

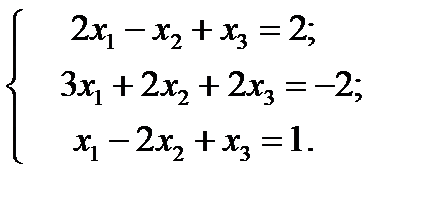
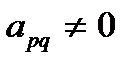 , для удобства вычислений берем
, для удобства вычислений берем  . Все элементы первой строки
. Все элементы первой строки 
 делим на этот разрешающий элемент. Все элементы разрешающего столбца
делим на этот разрешающий элемент. Все элементы разрешающего столбца 
 , кроме элемента
, кроме элемента  , обнуляем. Все остальные элементы таблицы вычисляем по правилу прямоугольника.
, обнуляем. Все остальные элементы таблицы вычисляем по правилу прямоугольника.




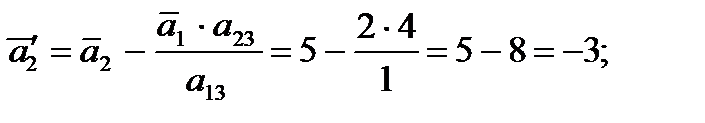

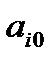

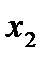





 , следовательно, переменную
, следовательно, переменную  записываем в базис.
записываем в базис. . Все элементы второй строки
. Все элементы второй строки 
 делим на этот разрешающий элемент. Все элементы разрешающего столбца
делим на этот разрешающий элемент. Все элементы разрешающего столбца 
 , кроме элемента
, кроме элемента  , обнуляем. Все остальные элементы таблицы вычисляем по правилу прямоугольника.
, обнуляем. Все остальные элементы таблицы вычисляем по правилу прямоугольника.



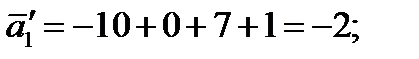

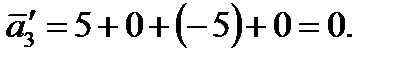
 , следовательно, переменную
, следовательно, переменную  записываем в базис.
записываем в базис. . Все элементы третьей строки
. Все элементы третьей строки 

 , кроме элемента
, кроме элемента  , обнуляем. Все остальные элементы таблицы вычисляем по правилу прямоугольника.
, обнуляем. Все остальные элементы таблицы вычисляем по правилу прямоугольника.




 , следовательно, переменную
, следовательно, переменную  записываем в базис.
записываем в базис.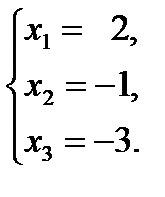
 .
. 2)
2) 
 4)
4)