Скалярное произведение векторов
1) 2) Если координатная форма скалярного произведения. 3) 4) 5) Пример 13.1. Даны вершины треугольника Найти косинус угла между сторонами Решение: По формуле:
Ответ: Пример 13.2. Дано разложение векторов 1) длины диагоналей параллелограмма, построенного на векторах 2) косинус угла между векторами
Решение: 1) Одна из диагоналей параллелограмма равна
Ответ: 2) Найдем косинус угла между векторами
Ответ: Решить задачи: 15. Найти скалярное произведение векторов 16. Найти скалярное произведение векторов 17. Найдите скалярное и векторное произведение векторов 18. Даны векторы 19. Найти угол между векторами 20. Векторы 21. Даны векторы б) ( 22. Даны три вектора 23. Даны вершины четырехугольника А(1; -2; 2), В(1; 4; 0), С(-4; 1; 1) и D(-5; -5; 3). Доказать, что его диагонали АС и BD взаимно перпендикулярны. 24. Вычислить какую работу производит сила 25. Даны вершины треугольника А(-1; -2; 4), В(-4; -2; 0) и С(3; -2; 1). Определить его внутренний угол при вершине B 26. Найти целое значение параметра m, при котором векторы
Практическое занятие 14
|

 .
. , то
, то  , -
, - ;
; ;
; .
.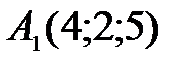 ;
;  ;
;  .
. и
и  .
. .
. .
. .
. и
и  по векторам
по векторам  и
и  . Требуется найти:
. Требуется найти: ,
,  ,
,  ,
,  ,
,  .
. , другая ─
, другая ─  .
. ,
, ,
,

 ;
;  .
. и
и  :
:
 .
. и
и  , если А(2;3;0), B(1;-1;2), C(1;-1;0) и D(1;1;1);
, если А(2;3;0), B(1;-1;2), C(1;-1;0) и D(1;1;1); .
. . Вычислите угол между ними.
. Вычислите угол между ними.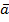 и
и  образуют угол
образуют угол  =
=  , зная, что |
, зная, что | 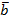 | = 4 вычислить (3
| = 4 вычислить (3  = 3
= 3  =
=  – b и
– b и  =
=  .
. = {4; -2; 4},
= {4; -2; 4},  )
)  .
. = {-1; 1; 4}. Вычислить
= {-1; 1; 4}. Вычислить 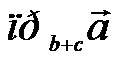 .
. = {3; -5; 2}, тогда её точка приложения перемещается из начала в конец вектора
= {3; -5; 2}, тогда её точка приложения перемещается из начала в конец вектора  = {2; -5; -7}
= {2; -5; -7} ортогональны.
ортогональны.


