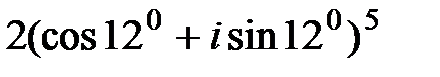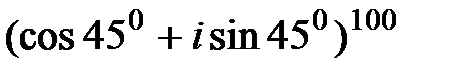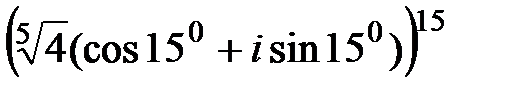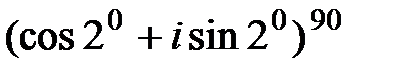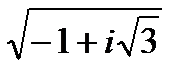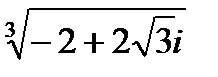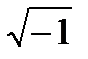Возведение в степень, извлечение корня.
52. Решить уравнение 1) 2) 3) 4) 5) 6) 7)
55. Изобразить геометрически комплексные числа: 1) z= 5 –2 i 2) z= –1 + i 3) z= 4 +2 i 4) z= 4 –2 i 5) z= –3 i 56. Найти модуль комплексного числа: 1) z= 1 +3 i. 2) z= 4 – i 3) z= 2 +3 i 57. Найти значение выражения: 1) (2 + 3 i)(5 – i) 2) (1 – i)(–3 + 2 i) 3) (–5 + i)(1 + 5 i) 58. Найти 1) 2) 3) 59. Найти 1) 2) 3) 4)
62. Результат операции деления числа z1 = 63. Результат операции деления числа z1 = 64. Найти 65. Найти
66. Вычислить значение функции: 1) 2) 3) 4)
67. Найти действительную часть комплексного числа: 1) 2) 68. Найти мнимую часть комплексного числа: 1) 2) 69. Найти число, сопряженное комплексному числу: 1) (2–7i)2 i 2) (1+2i)3 3) i (2 – 5 i)2
70. Записать комплексное число в алгебраической форме: 1) 2) 3) 4)
71. Записать комплексное число в тригонометрической форме: 1) 2) 3) 4) 72. Дано комплексное число z. Требуется записать число в алгебраической и тригонометрической формах.
73. Найти результат возведения в степень: 1) 2) 3) 4) 5) 6)
74. найти значения: 1) 2) 3) 4) 5) 6)
Практические занятия 17
|

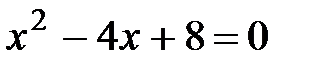

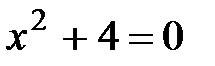

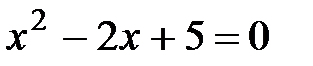
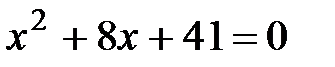
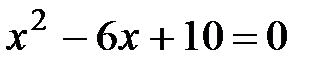
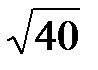
 , если
, если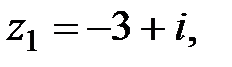
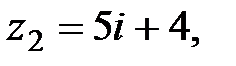
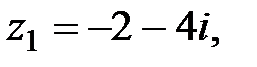
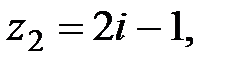

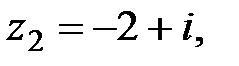
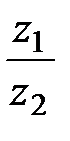 , если
, если

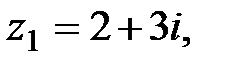
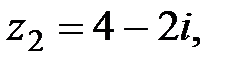

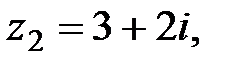

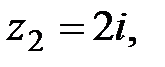
 (в градусах) равен
1) 2100 2) 98000
3) 20 4) 700
(в градусах) равен
1) 2100 2) 98000
3) 20 4) 700
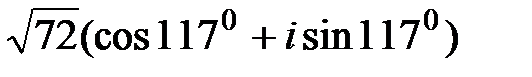 на число z2 =
на число z2 =  равен…
равен…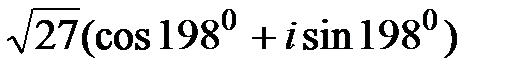 на число z2 =
на число z2 = 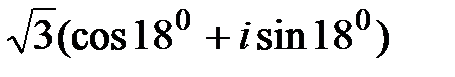 равен…
равен… , а z2 =
, а z2 = 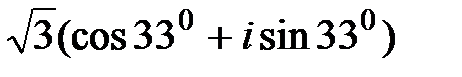 .
.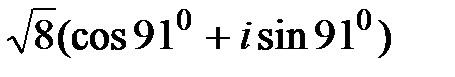 , а z2 =
, а z2 = 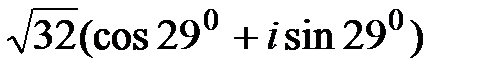 .
.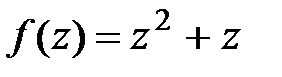 в точке z0 = 2 – i;
в точке z0 = 2 – i; в точке z0 = 1 + 5 i;
в точке z0 = 1 + 5 i;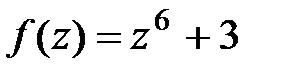 в точке z0 = i;
в точке z0 = i;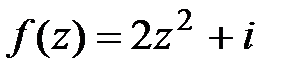 в точке z0 = 3 + i.
в точке z0 = 3 + i.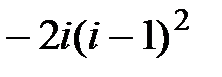
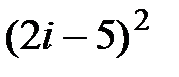
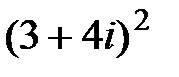
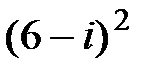
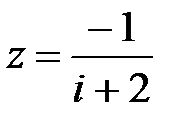
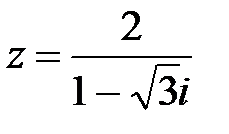
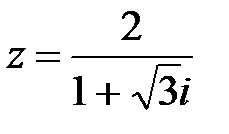


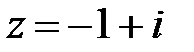

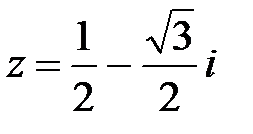
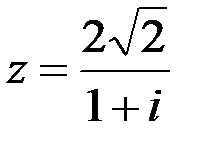 2.
2. 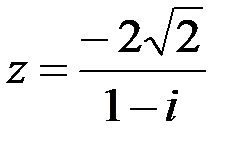 3.
3.  4.
4.  5.
5. 
 7.
7. 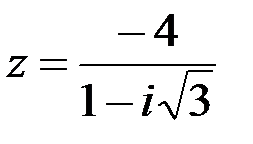 8.
8.  9.
9.  10.
10.