Гипербола
Основные теоретические сведения. Гипербола - геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная (не равная нулю и меньшая, чем расстояние между фокусами).
F1(-c,0), F2(c,0) – фокусы;
Решить задачи: 2.79. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметрично относительно начала координат, зная, кроме того, что: 1) её оси 2а = 10 и 2b = 8; 2) расстояние между фокусами 2с =10 и ось 2b = 8; 3) расстояние между фокусами 2 с = 6 и эксцентриситет ε = 4) ось 2 a = 16 и эксцентриситет ε = 5) уравнения асимптот y = ± и расстояние между фокусами 2с — 20; 6) расстояние между директрисами равно 22 — и расстояние между фокусами 2с = 26; 7) расстояние между директрисами равно 8) расстояние между директрисами равно 9) уравнения асимптот у = ± 2.80. Составить уравнение гиперболы, фокусы которой расположены на оси ординат, симметрично относительно начала координат, зная, кроме того, что: 1) её полуоси а = 6, b = 18 (буквой а мы обозначаем полуось гиперболы, расположенную на оси абсцисс); 2) расстояние между фокусами 2 с =10 и эксцентриситет ε = 3) уравнения асимптот у = ± 4) расстояние между директрисами равно 5) уравнения асимптот у = ± 2.81. Определить полуоси а и b каждой из следующих гипербол: 1) 4) х 2 — у 2 = 1; 5) 4 х 2 — 9 у 2 = 25; 6) 25 х 2 — 16 у 2 = 1; 7) 9 х 2 —16 у 2=1. 2.82.. Дана гипербола 16 х 2 — 9 у 2=144. Найти: 1) полуоси а и b; 2) фокусы; 3) эксцентриситет; 4) уравнения асимптот; 5) уравнения директрис. 2.83. Дана гипербола 16 х 2 — 9 у 2 = —144. Найти: 1) полуоси а и b; 2) фокусы; 3) эксцентриситет; 4) уравнения асимптот; 5) уравнения директрис. 9 х + 2 у — 24 = 0. 2.84. Установить, какие линии определяются следующими уравнениями: 1) y = + 3) х = — Изобразить эти линии на чертеже. 2.85. Дана точка М 1(10; — Составить уравнения прямых, на которых лежат фокальные радиусы точки M 1. 2.86. Убедившись, что точка М 1(— 5; определить фокальные радиусы точки M 1. 2.87. Эксцентриситет гиперболы ε = 2, фокальный радиус ей точки М, проведённый из некоторого фокуса, равен 16. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы. 2.88. Эксцентриситет гиперболы ε = 3, расстояние от точки М гиперболы до директрисы равно 4. Вычислить расстояние от точки М до фокуса, одностороннего с этой директрисой. 2.89. Определить точки гиперболы 2.90. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны: 1) точки M1(6; —1) и М2(—8; 2 2) точка M1(— 5; 3) гиперболы и эксцентриситет ε = 3) точка M1( 4) точка M1(—3; 5) уравнения асимптот у = ± 2.91. Фокусы гиперболы совпадают с фокусами эллипса Составить уравнение гиперболы, если её эксцентриситет ε = 2. 2.92. Составить уравнение гиперболы, фокусы которой лежат в вершинах эллипса до двух её асимптот есть величина постоянная, равная и прямыми, проведёнными через любую её точку параллельно асимптотам, есть величина постоянная, равная 2.93. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты её центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис: 1) 16х2 — 9у9 — 64х — 54у—161 = 0; 2) 9х2 — 16у2 + 90х + 32у — 367 = 0; 3) 16х2 — 9у2 — 64х—18у+199 = 0. 2.94. Установить, какие линии определяются следующими уравнениями: 1) у = — 1+ 3) х = 9 — 2 Изобразить эти линии на чертеже.
|


 каноническое уравнение гиперболы;
каноническое уравнение гиперболы; ;
; - эксцентриситет (ε>1);
- эксцентриситет (ε>1);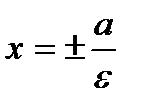 - уравнения директрис;
- уравнения директрис; - уравнения асимптот.
- уравнения асимптот. ;
; ;
;
 и ось 2b = 6;
и ось 2b = 6; и эксцентриситет ε =
и эксцентриситет ε =  и расстояние между директрисами равно 12
и расстояние между директрисами равно 12  516.
516. ;
; и расстояние между вершинами равно 48;
и расстояние между вершинами равно 48; и эксцентриситет ε =
и эксцентриситет ε =  ;
; .
. ; 2)
; 2)  3) х 2— 4 у 2 = 16;
3) х 2— 4 у 2 = 16;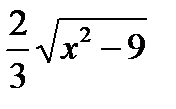 , 2) y = —3
, 2) y = —3  ,
, , 4) у = +
, 4) у = +  .
. ) на гиперболе
) на гиперболе  .
. ) лежит на гиперболе
) лежит на гиперболе  ,
,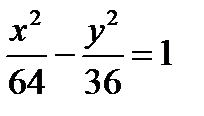 , расстояние которых до правого фокуса равно 4,5.
, расстояние которых до правого фокуса равно 4,5. ) гиперболы;
) гиперболы; ; —1) гиперболы и уравнения асимптот y = ±
; —1) гиперболы и уравнения асимптот y = ±  ;
; ) гиперболы и уравнения директрис y = ±
) гиперболы и уравнения директрис y = ±  ;
; ;
;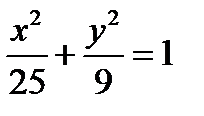
 = 1, а директрисы проходят через фокусы этого эллипса.
= 1, а директрисы проходят через фокусы этого эллипса. .
. .
. , 2) у = 7——
, 2) у = 7——  ,
, , 4) х = 5
, 4) х = 5  .
.


