Основные теоретические сведения. 1) -уравнение плоскости, проходящей через точку , перпендикулярно вектору - нормали к плоскости.
1)
2)
3) Если две плоскости заданы общими уравнениями:
то по уравнениям двух плоскостей можно определить их нормали На основании теоремы об углах, образованных взаимно перпендикулярными сторонами, один из углов между плоскостями можно определить как угол между нормалями по формуле:
Пример 1. Найти уравнение плоскости, проходящей через три заданные точки Решение: Составим уравнение плоскости
Ответ: Решить задачи: 2.108. Составить уравнение плоскости, которая проходит через точку M1(2; 1; —1) и имеет нормальный вектор n ={1, —2; 3}. 2.109. Составить уравнение плоскости, которая проходит через начало координат и имеет нормальный вектор п = {5; 0; —3}. 2.110. Точка Р (2; —1; —1) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравнение этой плоскости. 2.111. Даны две точки М1(3; —1; 2) и М2(4; —2; —1). Составить уравнение плоскости, проходящей через точку М1 перпендикулярно к вектору 2.112. Составить уравнение плоскости, проходящей через точку M1 (3;4; —5) параллельно двум векторам a1 = {3; 1; —1} и a2 = {1; —2; 1}. 2.113 Составить уравнение плоскости, проходящей через точки M 1(2; — 1; 3) и М 2(3; 1; 2) параллельно вектору а = {3; — 1; —4}. 2.114. Составить уравнение плоскости, проходящей через три точки: М 1 (3; — 1; 2), М 2 (4; — 1; — 1) и М 3 (2; 0; 2). 2.115. Определить координаты какого-нибудь нормального вектора каждой из следующих плоскостей. В каждом случае написать общее выражение координат произвольного нормального вектора: 1 ) 2х—у — 2z + 5 = 0; 2) х + 5у — z = 0; 3) 3х —2у —7 = 0; 4) 5у —3z = 0; 5)х + 2 = 0; 6) у — 3 = 0.
|

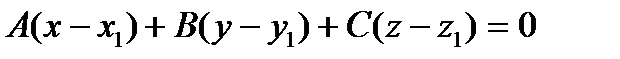 - уравнение плоскости, проходящей через точку
- уравнение плоскости, проходящей через точку  , перпендикулярно вектору
, перпендикулярно вектору  - нормали к плоскости.
- нормали к плоскости. -- уравнение плоскости, проходящей через три заданные точки
-- уравнение плоскости, проходящей через три заданные точки  .
.
 .
. .
.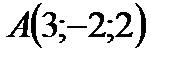 ;
; 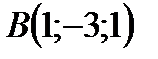 ;
;  .
. :
: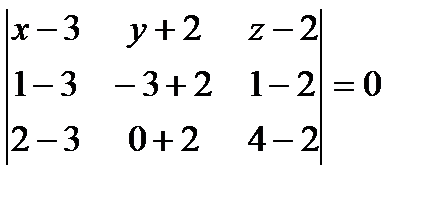 ,
,  ,
, ,
,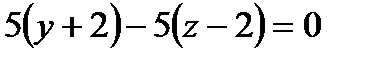 ,
, ,
,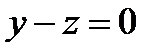 .
. .
. .
.


