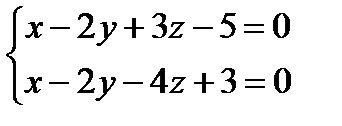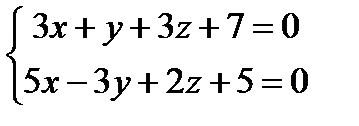Угол между прямой и плоскостью. Условия параллельности и перпендикулярности
Пример1. По координатам вершин пирамиды угол между ребром
Решение: Найдем угол между ребром
Ответ: Пример 2. Найти точку пересечения прямой
Решение: Координаты точки пересечения прямой
Решим эту систему методом Крамера:
Таким образом, точка пересечения прямой Ответ: Пример 3. Найти точку
Решение: Найдем точку
Далее найдем точку пересечения полученной прямой с данной плоскостью:
Нашли точку
Ответ: Решить задачи: 2.151. Доказать, что прямая х=3t — 2, у = — 4t+1, z= 4t — 5 параллельна плоскости 4х — 3у — 6z — 5 = 0. 2.152. Доказать, что прямая
лежит в плоскости 4х — Зу + 7z — 7 = 0. 2.153. Найти точку пересечения прямой и плоскости: 1) 2) 3) 2.154. Составить канонические уравнения прямой, проходящей через точку М0 (2; -4; -1) и середину отрезка прямой заключённого между плоскостями 2.155. Составить уравнения прямой, проходящей через точку М0 (2; — 3; — 5) перпендикулярно к плоскости 6х — Зу — 5z + 2 = 0. 2.156. Составить уравнение плоскости, проходящей через точку М0(1; —1; —1) перпендикулярно к прямой
2.157. Составить уравнение плоскости, проходящей через точку M0 (1; — 2; 1) перпендикулярно к прямой
2.158. При каком значении т прямая
параллельна плоскости х — Зу + 6z + 7 = 0? 2.159. При каком значении С прямая
параллельна плоскости 2x—у + Сz —2 = 0? 2.160. При каких значениях А и D прямая х=3 + 4t, у=1— 4t, z = — 3 +t лежит в плоскости Ах + 2у— 4z + D = 0? 2.161. При каких значениях А и В плоскость Ах + Ву + Зz — 5 = 0 перпендикулярна к прямой х = 3 + 2t, у = 5 —3t, z = — 2 — 2t? 2.162. При каких значениях t и С прямая
перпендикулярна к плоскости Зх — 2у + Сz+1=0? 2.163. Найти проекцию точки Р(2; — 1; 3) на прямую х=3t,, у=5t— 7, z = 2t + 2. 2.164. Найти точку Q, симметричную точке Р(4; 1; 6) относительно прямой
2.165. Найти точку Q, симметричную точке Р(2; —5; 7) относительно прямой, проходящей через точки M1 (5; 4; 6) и М2 (— 2; —17; —8). 2.170. Найти проекцию точки Р(5; 2; —1) на плоскость 2x-y+3z+23=0. 2.171. Найти точку Q, симметричную точке Р(1; 3; —4) относительно плоскости Зх+у — 2z = 0. 2.172. Составить уравнение плоскости, проходящей через точкуM1(1; 2; —3) параллельно прямым
2.173. Составить уравнение плоскости, проходящей через прямую x= — x=2t+1; y=-3t+2; z=2t-3 иточку M1 (2; —2; 1). 2.174. Составить уравнение плоскости, проходящей через две параллельные прямые
2.175. Найти точку Q, симметричную точке Р(3; —4; —6) относительно плоскости, проходящей через М1 (— 6; 1; —5), М2 (7; —2; —1) и М1 (10; —7; 1). 2.176. Найти точку Q, симметричную точке Р(— 3; 2; 5) относительно плоскости, проходящей через прямые
2.177. Составить уравнение плоскости, проходящей через прямую
перпендикулярно к плоскости Зх + 2у — z — 5 = 0.
|

 найти
найти и плоскостью основания
и плоскостью основания  :
: 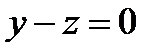 .
.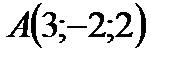 ;
; 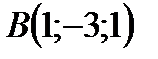 ;
;  ;
; 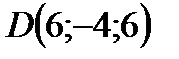 .
.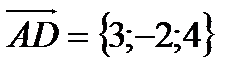 ,
, 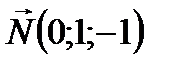 ,
, 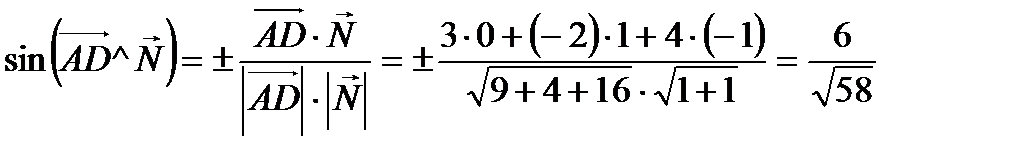 .
.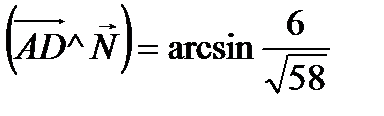 .
. , заданной общим уравнением, с данной плоскостью
, заданной общим уравнением, с данной плоскостью 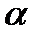 .
.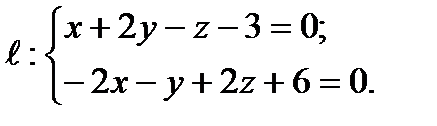
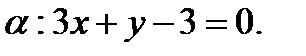
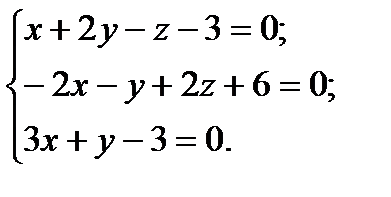

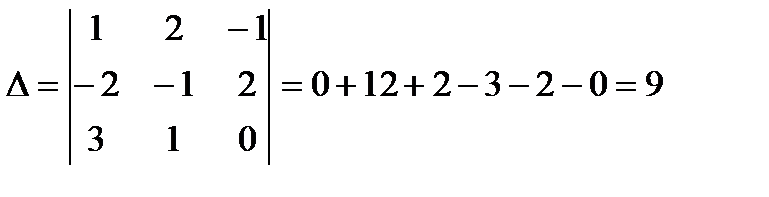 ,
,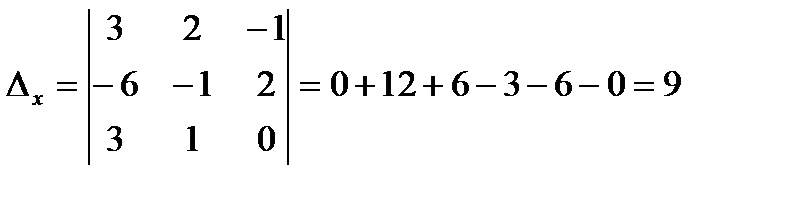 ,
,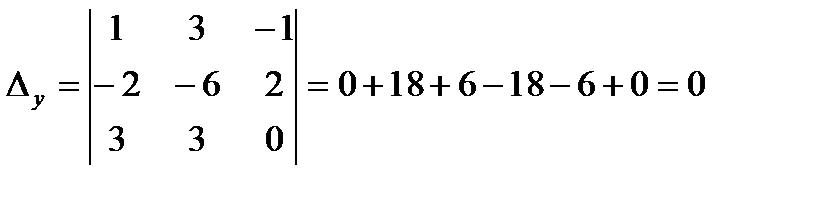 ,
,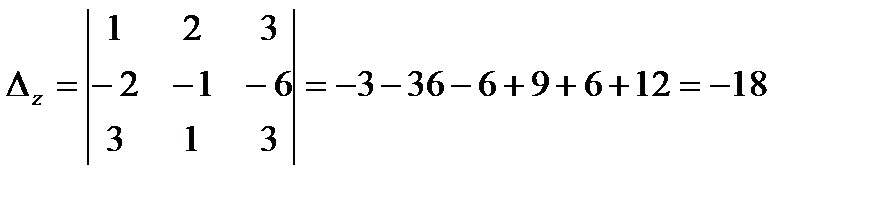 ,
,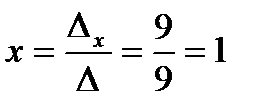 ,
, 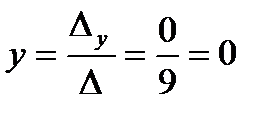 ,
, 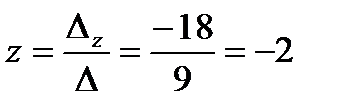 .
. .
.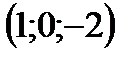
 , симметричную точке
, симметричную точке 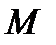 относительно плоскости
относительно плоскости 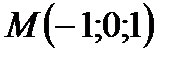 ,
, 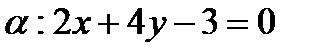 .
.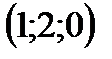 :
: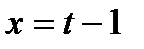 ,
, 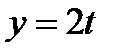 ,
, 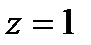 .
. ,
,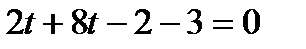 ,
, ,
,
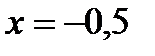 ,
, 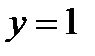 ,
, 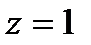 .
.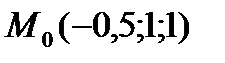 , которая является серединой отрезка
, которая является серединой отрезка 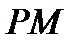 , поэтому
, поэтому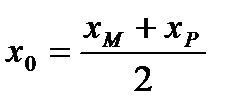 ,
, 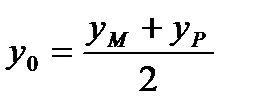 ,
, 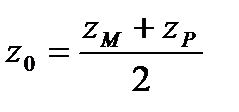 ,
,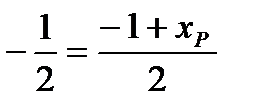 ,
, 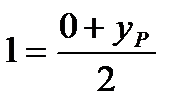 ,
, 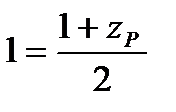 ,
,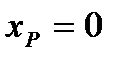 ,
, 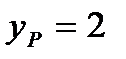 ,
, 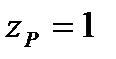 .
.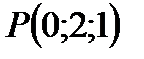 .
.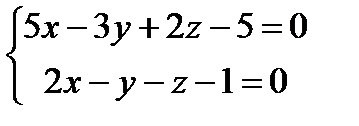
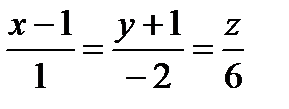 ,
, 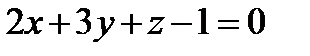 ;
;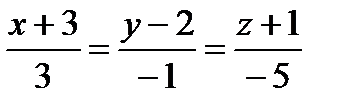 ,
, 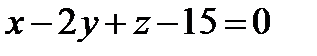 ;
; ,
, 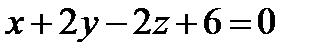 ;
;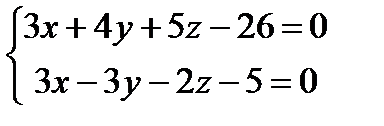
 ,
, 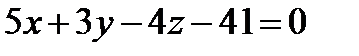 ,
,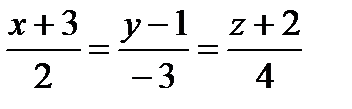 ,
,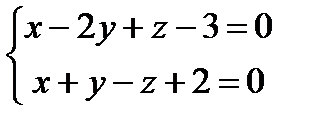
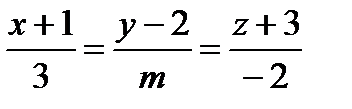 ,
,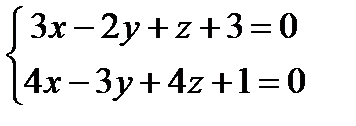
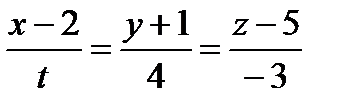

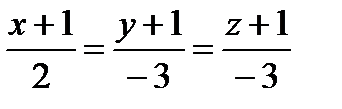 ,
, 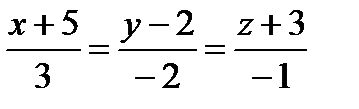
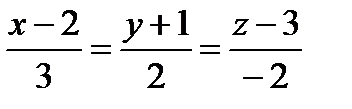 ,
,  .
.