Основные теоретические сведения.
1)
2) 3) y-y1=k(x-x1) уравнение пучка прямых с центром A(x1, y1) и угловым коэффициентом k. 4) y=kx+b уравнение прямой с угловым коэффициентом. 5) A(x-x1)+B(y-y1)=0 уравнение прямой, проходящей через точку После упрощения последнего уравнения получаем: Ax+By+C=0 - общее уравнение прямой, где C=-(Ax1+By1). Угловой коэффициент прямой находим по формуле Пример 1. Даны вершины треугольника 1) уравнение высоты, опущенной из вершины 2) точку пересечения высоты 3) точку пересечения медиан треугольника
Решение: 1) Составим уравнение высоты
Ответ:
2) Составим уравнение стороны
Найдем точку пересечения высоты
Ответ: 3) Найдем середину стороны
Составим уравнение прямой проходящей через точку
Найдем середину стороны
Составим уравнение прямой проходящей через точку
Найдем точку пересечения найденных медиан:
Ответ: Решить задачи: 2.1. Даны две точки А (3; -1) и В (2; 1). Определить координаты точки М, симметричной точки А относительно точки В. 2.2. Даны три вершины параллелограмма А (3; -5), В (5; -3), С (-1; 3). Определить четвертную вершину D, противоположную В. 2.3. Отрезок, ограниченный точками А (1; 3) и В (4; 3) разделен на три части. Определить координаты точек деления. 2.4. (Устно) Определить, какие из точек М1 (3; 1), М2 (2; 3), М4 (-3; -3), М5 (3; -1), М6 (-2; 1), лежали на прямой 2х – 3у – 3 = 0 и какие не лежат на ней. 2.5. Определить точки пересечения прямой 2х – 3у – 12 = 0 с координатными осями и построить эту прямую на чертеже. 2.6. Даны уравнения двух сторон параллелограмма 8х + 3у +1 = 0, 2х + у – 1=0, и уравнение одной из его диагоналей 3х + 2у + 3 = 0. Определить координаты вершин этого параллелограмма. 2.7. (Устно) Определить угловой коэффициент и отрезок в отсекаемый на оси ОУ, для каждой из прямых: 1) 5х – у + 3 = 0, 4) 3х + 2у = 0, 3) 5х + 3у + 2 = 0. 2.8. Даны уравнения двух сторон прямоугольника 2х – 3у + 5 = 0, 3х+ 2у – 7 = 0 и одна из его вершин А (2; -3). Составить уравнения двух других сторон этого прямоугольника. 2.9. Найти точку Q симметричную точке P (-5; 13) относительно прямой 2х –3у – 3 = 0. 2.10. Составить уравнения прямых, проходящих через вершины треугольника А (5; 4), В (-1; 3), С (-3; -2) параллельно противоположным сторонам. 2.11. Даны вершины треугольника А (1; -1), В (-2; 1) и С (3; 5). Составить уравнение перпендикуляра, опущенного из вершины А на медиану, проведенную из вершины В, длину этой медианы. Задание домой: Уравнение прямой линии. Расстояние от точки до прямой. 2.12. Даны две смежные вершины на параллелограмма А (-3; 5), В (1; 7) и точка пересечения его по диагонали М (1; 1). Определение две другие вершины. 2.13. Даны уравнения двух сторон прямоугольника х – 2у = 0, х – 2у + 15 = 0 и уравнение одной из его диагоналей 7х + у - 15 = 0. Найти вершины прямоугольника. 2.14. Найти проекции точки Р (-6; 4) на прямую 4х – 5у + 3 = 0. 2.15. Даны вершины треугольника М1 (2; 1), М2 (-1; 1), М3 (3; 2). Составить уравнения его высот. 2.16. Стороны треугольника даны уравнениями 4х – у – 7 = 0, х + 3у – 31 = 0, х + 5у – 7 = 0. Определить точку пересечения его высот.
|

 - каноническое уравнение прямой, проходящей через заданную точку A1(x1, y1), параллельно вектору
- каноническое уравнение прямой, проходящей через заданную точку A1(x1, y1), параллельно вектору  .
. - направляющий вектор.
- направляющий вектор. - уравнение прямой, проходящей через 2 заданные точки A(x1, y1), A(x2, y2).
- уравнение прямой, проходящей через 2 заданные точки A(x1, y1), A(x2, y2). перпендикулярно вектору
перпендикулярно вектору  (
( - нормаль прямой).
- нормаль прямой). .
. . Найти:
. Найти:  ;
; и стороны
и стороны  ;
;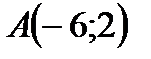 ;
;  ;
;  .
. :
: ;
; ,
, .
. ,
,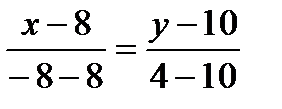 ,
, ,
, .
.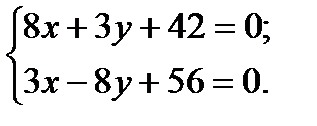




 .
. :
: ,
,  .
. ,
,  .
. и точку
и точку  :
: ,
,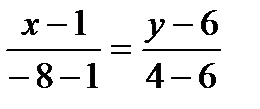 ,
, ,
, .
. :
: ,
, 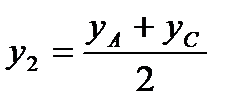 .
. ,
,  .
. :
: ,
, ,
, ,
, .
.


 .
.


