Решить задачи.
1.95. Составить уравнение параболы, вершина которой находится в начале координат, зная, что: 1) парабола расположена в правой полуплоскости, симметрично относительно оси Ох, и её параметр р = 3; 2) парабола расположена в левой полуплоскости, симметрично относительно оси Ох, и её параметр р = 0,5; 3) парабола расположена в верхней полуплоскости, симметрично относительно оси Оу, и её параметр p = 4) парабола расположена в нижней полуплоскости, симметрично относительно оси Оу, и её параметр р =3. 2.96. Определить величину параметра и расположение относительно координатных осей следующих парабол: 1) у 2 = 6 х; 2) х 2 = 5 у; 3) у 2 = — 4 х; 4) х 2 = — у. 2.97. Составить уравнение параболы, вершина которой находится в начале координат, зная, что: 1) парабола симметрично расположена относительно оси Ох и проходит через точку А (9; 6); 2) парабола симметрично расположена относительно оси Ох и проходит через точку В(— 1; 3); 3) парабола симметрично расположена относительно оси Оу и проходит через точку С(1; 1); 4) парабола симметрично расположена относительно оси Оу и проходит через точку D (4; — 8). 2.98. Установить, какие линии определяются следующими уравнениями: 1) у = + 2 4) у = — 2 7) х = — Изобразить эти линии на чертеже. 2.99. Составить уравнение параболы, если дан фокус F(— 7; 0) и уравнение директрисы х —7 = 0. 2.100. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты её вершины А, величину параметра р и уравнение директрисы: 1) у 2 = 4 х — 8, 2) у 2 = 4 — 6 х, 3) х 2 = 6 у + 2, 4) х 2 = 2— у. 2.101. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты её вершины А и величину параметра р: 1) y = 3) y = — 2.102. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты её вершины А и величину параметра р: 1) х = 2 у 2 — 12 у + 14, 2) х = — 3) х = — у 2 + 2 у — 1. 2.103. Установить, какие линии определяются следующими уравнениями: 1) у = 3 — 4 3) х = 2 — Изобразить эти линии на чертеже. 2.104. Составить уравнение параболы, если даны её фокус F(7; 2) и директриса х — 5 = 0. 2.105. Составить уравнение параболы, если даны её фокус F(4; 3) и директриса у + 1 = 0. 2.106. Составить уравнение параболы, если даны её фокус F(2; — 1) и директриса х — у — 1 = 0. 2.107. Уравнения следующих кривых привести к каноническому виду, изобразить системы координат и кривые на чертеже. 1) 2х² + 5у² - 12х +10у + 13 = 0, 2) х² - у² + 6х + 4у – 4 + 0, 3) х ²– 10х = 4у – 13, 4) 3х² + 10ху + 3у² - 12х – 12у = 4 = 0, 5) х² - ху + у² - 3 = 0.
|

 ;
; , 2) у = +
, 2) у = +  , 3) у = — 3
, 3) у = — 3  ,
,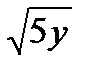 , 6) х = — 5
, 6) х = — 5  ,
, , 8) х = + 4
, 8) х = + 4  .
.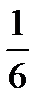 х 2 + 2 х — 7.
х 2 + 2 х — 7.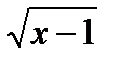 , 2) х = — 4 + 3
, 2) х = — 4 + 3  ,
,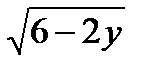 , 4) у = — 5 —
, 4) у = — 5 — 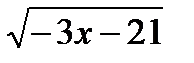 .
.


