Решение систем линейных уравнений методом Гаусса
Метод Гаусса решения систем линейных уравнений заключается в приведении системы уравнений к треугольному виду путем элементарных преобразований уравнений системы, к которым относятся: - перестановка двух уравнений; - умножение обеих частей одного из уравнений на ненулевое число; - прибавление к обеим частям одного из уравнений соответствующих частей другого уравнения. Элементарные преобразования переводят данную систему в эквивалентную ей.
Пример 9.1.. Решить системы линейных уравнений методом Гаусса. 1) Решение: Решим систему методом Гаусса. Первое уравнение системы оставляем без изменения, для получения второго уравнения умножим первое на 2 и сложим со вторым, а для получения третьего - умножим первое на 6 и сложим с третьим:
Первых два уравнения оставим без изменения, а для получения третьего умножим второе на 7 и сложим с третьим:
Ответ:
2) Ответ: решений нет.
3) Ответ: Бесчисленное множество решений:
Решить задачи: 1.111. Решите систему линейных уравнений: 1.112. Решите систему линейных уравнений: 1.113. Решите систему линейных уравнений: 1.114. Решите систему линейных уравнений: 1.115. Решите систему линейных уравнений: 1.116. Решите систему линейных уравнений: Практическое занятие 10
|



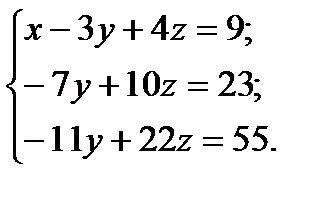






 ;
;  ;
;  .
.







 .
.








