Правило Крамера решения систем линейных уравнений третьего порядка.
Для систем трех уравнений с тремя неизвестными
правило Крамера имеет вид:
где
Пример 4.4.. Дана система трех линейных уравнений с тремя неизвестными. Требуется найти ее решение с помощью формул Крамера.
Решение: Найдем сначала главный определитель системы:
Так как главный определитель системы отличен от нуля, то система имеет единственное решение. Для нахождения решения по правилу Крамера найдем вспомогательные определители:
Таким образом, получаем:
Ответ:
Решить задачи: 1.63. Найти решение системы с помощью формул Крамера: 1.64. Найти решение системы с помощью формул Крамера: 1.65. Найти решение системы с помощью формул Крамера: 1.66. Решите систему линейных уравнений: 1.67. Решите систему линейных уравнений: 1.68. Решите систему линейных уравнений: 1.69. Решите систему линейных уравнений: 1.70. Решите систему линейных уравнений: 1.71. Решите систему линейных уравнений: 1.72. Решите систему линейных уравнений: 1.73. Решите систему линейных уравнений: 1.74. Решите систему линейных уравнений: 1.75. Найти все решения системы
1.76. Найти всерешения системы
1.77. Найти все решения системы
1.78. Определить, при каких значениях а и b система уравнений
1) имеет единственное решение; 2) не имеет решений; 3) имеет бесконечно много решений. 1.79. Доказать, что если система уравнений совместна, то 1.80. Найти все решения системы 1.81. Найти все решения системы 1.82. Определить, при каком значении а система однородныхуравнений
|


 ,
,

 .
. ;
; ;
; .
. ;
;  ;
;  .
. ;
;  ;
;  .
.









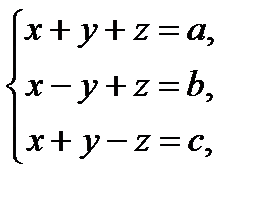
 .
.




 = 0
= 0
 имеет ненулевое решение.
имеет ненулевое решение.


