Моделювання процесів в складних медико-біологічних системах
Звернемося спочатку до якісного аналізу динамічної системи, що описується двома нелінійними диференціальними рівняннями довільного вигляду:
Дослідимо стійкість стаціонарного стану такої системи, застосовуючи метод малих збурень і лінеаризації диференціальних рівнянь. Для цієї мети представимо розв’язок у вигляді суми стаціонарних значень змінних х 0, у 0 і малих збурень z, h: х = х 0 + z, у = у 0 + h. Лінеаризуючи систему диференціальних рівнянь, тобто залишаючи лише ті доданки, що містять перші степені малих збурень z, h, отримуємо
де коефіцієнти а, b, c, d пов’язані з похідними
Важливе значення в якісному аналізі поведінки динамічних систем відіграє часова еволюція послідовних станів досліджуваної системи у вигляді траєкторії руху зображуючої точки у фазовому просторі х, у. Така траєкторія називається фазовим портретом, або фазовою кривою системи. В залежності від вигляду фазового портрету динамічні системи поділяються, як вже вказувалося раніше, на грубі та негрубі. “Грубі” системи – це системи, характер траєкторії яких у фазовому просторі зберігається при малих змінах похідних а, b, c, d. “Негрубі” системи – це такі, траєкторії яких відчувають достатньо різкі якісні зміни при малих варіаціях параметрів а, b, c, d. Будемо шукати загальний розв’язок досліджуваної динамічної системи поблизу її стаціонарного стану у вигляді z = А ехр (l t), h = B ехр (l t). Тоді
звідки маємо lА = аА + bB, lB = cA + dB. Ненульовий розв’язок даної алгебраїчної системи рівнянь відносно коефіцієнтів А і В має місце лише при умові, що головний визначник рівний нулю:
або Звідси для коренів цього рівняння, яке зветься характеристичним, маємо l 1, 2 = [(a + d)/2] ± {[(a + d)2/4] – (ad – bc)}1/2. Якщо корені не є кратними, то розв’язок системи може бути подано у такому вигляді:
Нехай корені l 1, l 2 – дійсні. Тоді особливі точки у відповідності з класифікацією Пуанкаре (див. табл. 7.4) являють собою вузли або сідла, а саме: а) l 1 < 0, l 2 < 0 – стійкий вузол; б) l 1 > 0, l 2 > 0 – нестійкий вузол; в) l 1 > 0, l 2 < 0 або l 1 < 0, l 2 > 0 – особлива нестійка точка, яка називається “ сідлом ”; г) якщо l 1, l 2 – комплексно-спряжені величини, тоді у системі відбуваються коливання; особлива точка – фокус, причому, якщо Re l 1,2 < 0 – стійкий фокус, якщо Re l 1,2 > 0 – нестійкий фокус. д) якщо Re l = 0, то у системі відбуваються незатухаючі коливання; особлива точка – центр або граничний цикл. Зауважимо, що стійкий і нестійкий вузли, стійкий і нестійкий фокуси, а також сідла характеризують “грубі” системи, тоді як граничний цикл (центр) – “негрубі”. Як вже зазначалося, поблизу критичних (біфуркаційних) точок малі зміни зовнішніх параметрів можуть призвести до якісних перебудов (біфуркацій) фазових портретів досліджуваних систем. Розглянемо найбільш типові біфуркації: 1. Біфуркація з одного вузла (фокуса) в два вузла (фокуса). За певних умов розв’язки, що відповідають стійкому вузлу (фокусу), можуть стати нестійкими і відбувається перехід у два нових стійких вузла. При відмінній від нуля уявній частині коренів характеристичного рівняння вузли перетворюються, очевидно, в фокуси. 2. Біфуркація Хопфа із фокуса в граничний цикл. Для цього випадку, вивченого вперше Хопфом, корені характеристичного рівняння є комплексно-спряженими числами l 1 = Re l 1 + i Im l 1 , l 2 = Re l 2 – i Im l 2. ПриRe l ® 0 корені наближаються до уявної вісі. У результаті первинно стійкий фокус перетворюється у граничний цикл, тобто у системі виникають періодичні в часі коливання. 3. Біфуркації граничного циклу. При подальшій зміні керуючих параметрів можуть відбутися нові перебудови фазових траєкторій системи, при яких можливі такі біфуркації: а) старий граничний цикл переходить в новий один або більше граничних циклів у одній і тій самій площині; б) старий двовимірний граничний цикл переходить у тривимірний граничний цикл, до того ж у випадку незамкнутих траєкторій виникає рух зображуючої точки по поверхні тора; в) старий граничний цикл з періодом Т 1 переходить у новий, рухаючись по якому система повертається у початковий стан за час Т 2 = 2 Т 1 (біфуркація подвоєння періоду).
Зручним методом аналізу стійкості фазових траєкторій є дослідження так званих показників Ляпунова. Не вдаючись у достатньо тонкі і складні математичні деталі, показники Ляпунова можна визначити як узагальнення показника степені у виразі для експоненціального в часі розв’язку d х (t), який характеризує диференціальне рівняння першого порядку довільного вигляду, а саме:
Кількість показників Ляпунова не повинна перевищувати розмірність простору, в якому задана шукана величина d x (t).Тоді виявляється можливим сформулювати такі критерії для простих і дивних аттракторів у термінах показників Ляпунова (розглянемо для визначення тривимірний випадок): а) якщо всі три показники Ляпунова від’ємні, то аттрактор – стійкий фокус; б) якщо два показники від’ємні, а третій рівний нулю, то аттрактор – граничний цикл; в) якщо один показник від’ємний, а два інші дорівнюють нулю, то аттрактор – стійкий тор; г) якщо один з показників Ляпунова виявляється додатнім, то стає можливим хаотичний рух зображуючої точки. Так, при l 1 > 0, l 2 = 0, l 3 < 0 виникає дивний (хаотичний) аттрактор, до того ж фазові сусідні траєкторії швидко розходяться при незначній зміні початкових умов. Одним з перших прикладів дивного аттрактора стала гідродинамічна (метеорологічна) модель Лоренца, розв’язки якої виявили хаотичне розбігання фазових траєкторій в силу ефектів турбулентності і неточності задання початкових умов. Зауважимо, що при l 1 > 0, l 2 = l 3 = 0 або при l 1 > 0, l 2 > 0, l 3 = 0 фазові портрети системи є відповідно нестійкий тор або нестійкий граничний цикл, які не є аттракторами. Для встановлення універсальних закономірностей в самоорганізованих системах, які мають різні геометричні розміри, розуміння ролі їх спонтанного ускладнення, наявності в них просторово корельованих областей широко залучаються методи кінетичних моделей, які були покладені в основу сучасної теорії дисипативних структур (І.Р. Пригожин, Г. Ніколіс, П. Гленсдорф та інші). В якості конкретного прикладу кінетичної моделі розглянемо відому модель “ хижак-жертва ”, яку запропонували А. Лотка і В. Вольтера. Система нелінійних диференціальних рівнянь цієї моделі має вигляд:
Перше рівняння описує динаміку чисельності першого типу тварин – “жертв“ (наприклад, зайців), які живляться рослинами. Перший доданок у правій частині цього рівняння описує природне розмноження жертв, тоді як другий – їх зменшення від зустрічей з “хижаками“ (наприклад, рисями). Друге рівняння характеризує динаміку зміни чисельності хижаків: перший доданок у правій частині задає збільшення хижаків, які живляться жертвами, а другий – природне зменшення жертв при відсутності цієї їжі. Проведемо аналіз моделі “хижак-жертва“. Стаціонарний розв’язок моделі визначається з наступної системи рівнянь:
Лінеаризація рівнянь системи (7.21) поблизу стаціонарного розв’язку дає
Шукаючи розв’язок цієї системи у вигляді ζ = А ехр (l t), h = B exp (l t), (7.24) отримуємо характеристичне рівняння:
або l 2 + e 1 e 2 = 0, звідки отримуємо шукані корені l 1,2 = ± і (e 1 e 2)1/2. (7.25) Таким чином, у відповідності до класифікації особливих точок по А. Пуанкаре отримана особлива точка в моделі “хижак-жертва“ є центр (або граничний цикл). Фазові криві являють собою замкнуті траєкторії. Оскільки для малих збурень ζ;(t) і h (t) мають місце співвідношення вигляду
то цей результат відображає те, що ми спостерігаємо в реальних умовах, тобто експериментально, а саме: періодичну зміну чисельності популяцій хижаків і жертв (див. мал. 7.11).
Мал. 7.11. Періодична зміна чисельності популяції в екологічній системі “хижак(рисі) - жертва (зайці)” за даними “Хадсон-Бей” (з книги Г. Хакена “Синергетика”). Недолік розглянутої вище моделі Лотка-Вольтерра – її “негрубість“. Іншими словами, випадкові зміни чисельності одного з видів змінюють амплітуди коливань кожного виду. В реальності такого не спостерігається. Покращання моделі Лотка-Вольтерра пов’язане з врахуванням самообмежень в зростанні чисельності обох популяцій, що описується введенням останніх (третіх) доданків в рівняння моделі
Дослідження особливих точок для такої покращаної моделі показує, що якщо при g 11 = g 22 = 0 особлива точка являла собою центр або граничний цикл (негруба система), то при g 11 ¹ 0, g 22 ¹ 0 особлива точка є вже стійкий фокус або стійкий вузол, тобто система стає грубою. Ще одним популярним прикладом кінетичних моделей процесів самоорганізації, як вже відзначалося, є модель “брюселятора“ (Пригожин, Ніколіс, Лефевр), яка описує хімічний автокаталітичний процес. Близька до “брюселятора“ кінетична модель “орегонатора“ була запропонована і досліджена Філдом і Ноейсом. Зокрема, модель “орегонатора“ описує автохвильові процеси, які виникають в періодичній окисно-відновній реакції Бєлоусова-Жаботинського. 7.5. Практичне заняття “Термодинаміка відкритих біологічних систем” Мета заняття: 1. Вивчити основні положення термодинаміки відкритих біологічних систем, що обмінюються речовиною та енергією з оточуючим середовищем. 2. Навчитися застосовувати термодинамічні методи для дослідження відкритих медико-біологічних систем. Теоретичні питання, що розглядаються на практичному занятті 1. Термодинамічний метод вивчення медико-біологічних систем. 2. Термодинаміка рівноважних ізольованих систем. 3. Перший та другий закони (начала) термодинаміки. 4. Ентропія, зв’язок ентропії з термодинамічною ймовірністю (принцип Больцмана). 5. Термодинамічні потенціали. 6. Термодинаміка відкритих систем поблизу положення рівноваги. 6.1. Лінійний закон для потоків і термодинамічних сил. 6.2. Перехресні процеси переносу, принцип симетрії кінетичних коефіцієнтів. 6.3. Виробництво ентропії. 6.4. Спряження потоків. 6.5. Стаціонарний стан відкритих систем, теорема Пригожина. 7. Термодинаміка відкритих систем, далеких від положення рівноваги. Процеси впорядкування в системах різної природи. Поняття про синергетику.
|

 (7.19)
(7.19) (7.20)
(7.20)

 ,
, .
. (7.21)
(7.21) 4. Дивні аттрактори. При зміні керуючих параметрів фазова траєкторія, що являє собою рух по тору, може стати нестійкою і хаотичною. У цьому випадку, який отримав назву дивного аттрактора, траекторії руху зображуючої точки у фазовій площині стають недетермінованими (мал. 7.10). Якщо для простих аттракторів (стійких особливих точок і граничних циклів) усі фазові траєкторії стягуються у близьке оточення цих точок або граничного циклу, то для дивного аттрактора усі фазові траєкторії розбігаються і хаотично перемішуються, залишаючись в області тяжіння дивного аттрактора.
4. Дивні аттрактори. При зміні керуючих параметрів фазова траєкторія, що являє собою рух по тору, може стати нестійкою і хаотичною. У цьому випадку, який отримав назву дивного аттрактора, траекторії руху зображуючої точки у фазовій площині стають недетермінованими (мал. 7.10). Якщо для простих аттракторів (стійких особливих точок і граничних циклів) усі фазові траєкторії стягуються у близьке оточення цих точок або граничного циклу, то для дивного аттрактора усі фазові траєкторії розбігаються і хаотично перемішуються, залишаючись в області тяжіння дивного аттрактора. .
. (7.21)
(7.21) (7.22)
(7.22) (7.23)
(7.23)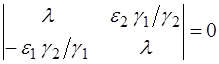 ,
, (7.26)
(7.26)
 (7.27)
(7.27)


