Закотилися вівці в долинку, і тут тихіше.

Дата добавления: 2015-10-15; просмотров: 817

Определение 2. Множество всех первообразных данной функции f(x) на интервале (a;b) называется неопределенным интегралом функции f(x) на этом интервале и обозначается символом:

В обозначении 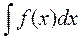знак называется знаком интеграла, 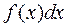- подынтегральным выражением, - подынтегральной функцией, - переменной интегрирования.

Теорема 2. Если функция f(x) непрерывна на (a;b), то она имеет на (a;b) первообразную и неопределенный интеграл.

Замечание. Операция нахождения неопределенного интеграла от данной функции f(x) на некотором промежутке носит название интегрирования функции f(x).

Свойства неопределенного интеграла.

Из определений первообразной F(x) неопределенного интеграла от данной функции f(x) на некотором промежутке следуют свойства неопределенного интеграла:

1. .

2. .

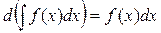3. , где С – произвольная постоянная.

4. , где k = const.

5.

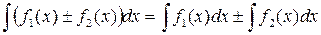
Замечание. Все вышеперечисленные свойства верны при условии. Что интегралы, фигурирующие в них, рассматриваются на одном и том же промежутке и существуют.

Таблица основных неопределенных интегралов.

Действие интегрирования является обратным действию дифференцирования, то есть по заданной производной f(x) надо восстановить начальную функцию F(x). Тогда из определения 2 и таблицы производных получается таблица основных интегралов.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

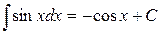8. .

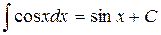9. .

10. .

11. .

12. .

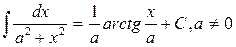13. .

14. .

15. .

16. .

В формулах 1-16 С – произвольная постоянная.

Замечание. Интеграл не от любой элементарной функции является элементарной функцией. Параметрами могут служить следующие интегралы, часто встречающиеся в задачах:

- интеграл Пуассона,

- интеграл Френеля,

- интегральный логарифм,

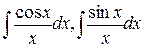
- интегральный косинус и синус.

Указанные функции существуют, имеют важное прикладное значение. Для них составлены таблицы значений.