Але хмара тільки моргнула зневажливо лівим крилом і почала завертати направо, понад царинки.

Дата добавления: 2015-10-15; просмотров: 833

Теорема 4.Пусть функция f (x) непрерывна на [a;b] и F (x) – какая-либо ее первообразная на [a;b]. Тогда определенный интеграл от функции f (x) по отрезку [a;b] равен разности значений функции F(x) в точках b и a: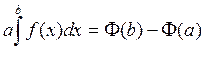

Доказательство. Из теоремы 3 следует, что наряду с функцией F(x) функция 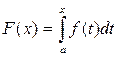также является на [a;b] первообразной для f (x). Тогда по свойству первообразных для одной и той же функции на некоторой области имеем:

для любого xÎ [a;b] (**)

Вычислим значение const. Для этого, используя свойство 1 определенного интеграла , рассмотрим равенство (**) при x = a:

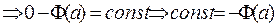
Следовательно, равенство (**) можно переписать в виде:

для xÎ [a;b]

Теперь рассмотрим полученное равенство при x = b:

Это и есть формула Ньютона-Лейбница. Она является основной формулой интегрального исчисления, устанавливающей связь между определенным и неопределенным интегралами и дает правило вычисления определенного интеграла.

Замечание. Формулу Ньютона-Лейбница часто записывают в виде:

,

Где используется обозначение:

.

Вычисление определенного интеграла с помощью формулы Ньютона-Лейбница

Задача вычисления определенного интеграла свелась к нахождению первообразной непрерывной функции.

Пример 1.

Ответ:

Пример 2.

Ответ: