
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Що чути селом?
Дата добавления: 2015-10-15; просмотров: 1008
|
|
1) Разложение рациональной дроби на сумму простых дробей.
Определение 1. Рациональной дробью называется отношение двух многочленов:
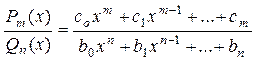


Определение 2. Рациональная дробь называется правильной, если m<n. В противном случае (если m ³ n) она называется неправильной.
Определение 3. Простыми рациональными дробями называются дроби следующих четырех типов:
I  .
.
II 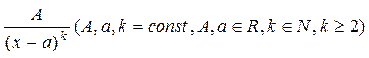 .
.
III 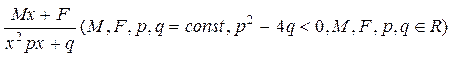
IV 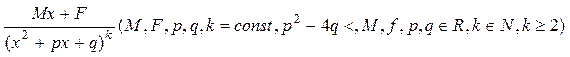
Теорема 3. Всякую неправильную рациональную дробь можно представить в виде суммы целой части (многочлена) и правильной рациональной дроби.
Пример 20. Представить дробь 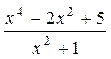 в виде суммы целой части и правильной рациональной дроби.
в виде суммы целой части и правильной рациональной дроби.
Так как высшая степень числителя равна 4, а знаменателя – 2, то данная дробь неправильная (4 > 2). Разделим числитель на знаменатель:
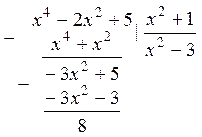
Следовательно, дробь можно записать в виде:
 .
.
Ответ: 
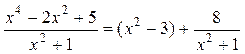 .
.
Теорема 4. Любую правильную рациональную дробь можно единственным образом представить в виде суммы конечного числа простых рациональных дробей.
Разложение правильной рациональной дроби 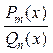 (m<n) на сумму простых дробей выполняют по следующей схеме:
(m<n) на сумму простых дробей выполняют по следующей схеме:
а) Найти корни многочлена Qn(x) и представить его в виде произведения простых множителей:
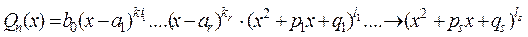 ,
,
Где 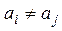 ,
, 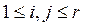
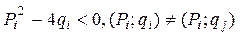 ,
, 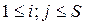
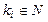 ,
, 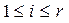
 ,
, 
б) Записать разложение дроби с неопределенными коэффициентами:

в) Определить коэффициенты
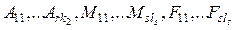
суммарное число которых равно n, методом неопределенных коэффициентов.
Для этого необходимо все разложение привести к общему знаменателю и приравнять числитель полученной дроби Pm(x). Приравнивания в этих многочленах коэффициенты при одинаковых степенях x, получим систему из n линейных уравнений с n неизвестными. Эта система имеет единственное решение – интересующие нас коэффициенты.
Пример 21. Разложить дробь 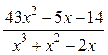 на сумму простых дробей.
на сумму простых дробей.
1) Данная дробь правильная. Разложим знаменатель на множители:
 .
.
2) Запишем разложение данной дроби на сумму простых дробей:

3) Для нахождения коэффициентов A, B и C приводим разложение к общему знаменателю и приравняем их числители.
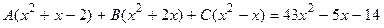
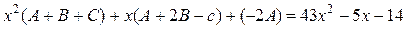
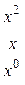
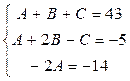



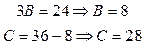
Следовательно:
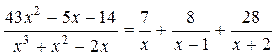
| <== предыдущая лекция | | | следующая лекция ==> |
| Розспівався! - сердиться ватаг і наново перелічує карби. | | | Чи не пора варити кулешу на сніданок для вівчарів? |