Як спали, Палагночко, душко?

Дата добавления: 2015-10-15; просмотров: 778

1)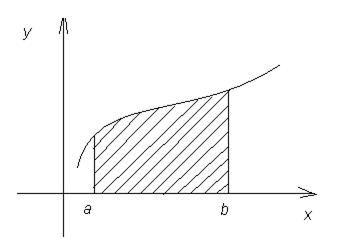

.

2) Если область ограничена двумя кривыми y = f (x) и y = g (x), причем при xÎ [a;b] f (x) ³ g (x), то площадь области ограниченным кривыми y = f (x); y = g (x) и прямыми x = a, x = b вычисляется по формуле:

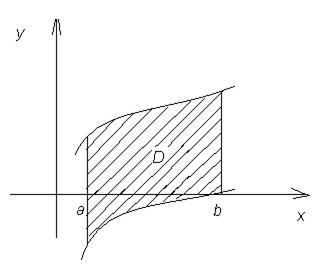
Свойства определенного интеграла.

1)

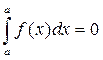
2)

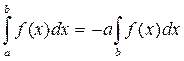
3)

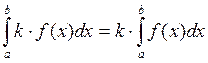
4)

5) Если функция f (x) интегрируема на отрезках [a;c] и [c;b], то она интегрируема и на [a;b], причем верно равенство:

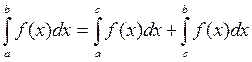
При любом расположении точек a, b и c на оси Ox.

6) Если f (x) ³ 0 при xÎ [a;b], то

7) Если на [a;b] f (x) ³ g (x), то

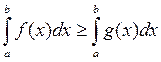
8) Теорема 2 (о среднем значении определенного интеграла).

Если функция f (x) непрерывна на [a;b], то на этом отрезке найдется хотя бы одна точка c, в которой выполняется равенство:

Доказательство:Так как f (x) на [a;b] непрерывна, то она достигает на этом отрезке своих наименьшего “m” и наибольшего “M” значений. Тогда m £ f (x) £ M для любого x Î [a;b]. По свойству 7 определенного интеграла можно записать неравенство:

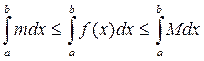
Так как m и M – постоянные числа, то

(*)

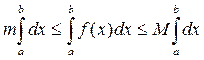Вычислим по определению определенного интеграла

Тогда неравенство (*) можно переписать:

Разделим все части полученного неравенства на (b - a) > 0 (длина отрезка интегрирования):

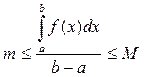
Так как f (x) непрерывна на [a;b], тона принимает все значения, заключенные между наименьшим “m” и наибольшим “M” значениями. Значит найдется на [a;b] хотя бы одна точка c, в которой выполняется равенство:

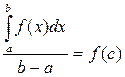
Вычисление определенного интеграла