Свойства параллельных проекцийПроекция прямой линии есть прямая линия (Рис.1.3). Плоскость, определяемая двумя пересекающимися прямыми АВ и ААр, пересекает плоскость проекций Р по прямой АрВр. Исключение составляет проекция прямой линии, которая параллельна направлению проецирования. Такая прямая проецируется в точку (Рис.1.3). Следствия из свойства. Если точка лежит на прямой, то ее проекции лежат на соответствующих проекциях прямой (Рис.1.3). Если две прямые пересекаются, т.е. проходят через одну точку Е, то и соответствующие проекции этих прямых пересекаются, проходят через проекции точек пересечения Ер (Рис.1.4). Если прямые АВ и СD параллельны, то и соответствующие их проекции параллельны, т.е. АрВр ÷ ÷ CpDp (Рис.1.5). Отношение отрезков параллельных прямых равно отношению их проекций: Отношение отрезков прямой равно отношению их проекций (Рис.1.7).
Рис. 1.3. Проекции прямых линий Рис. 1.4. Проекции пересе-
|
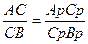(Рис.1.6).
