Сіңкілік қатардың тегістеу тәсілі
Ә леуметтік – экономикалық қ ұ былыстардың даму немесе кему бағ ыттарын айқ ындау, кө п мә нді аналитикалық тегістеу тә сіліне негізделген. Ө сің кілік қ атарлар кө рсеткіштерін тегістеу ең кіші шаршы (квадрат) тә сілі арқ ылы жү ргізіледі. Егер зерттеуге алынғ ан ө сің кілік қ атар бірқ алыпты нақ ты ө згеріп отыратын болса, онда қ атарды тегістеу ү шін тү зу сызық ты ө ң деу қ олданады. Егер тұ рақ ты тү рде қ арқ ын ө сіп отырса, онда қ исық, ал ү демелі тү рде нақ ты артып отыратын болса, онда екінші дең гейдегі парабола қ олданылады.10.4. кесте аналитикалық тегістеу ү шін ең жиі қ олданатын тренд модельдерінің тү рлері берілген.
Кесте 4. - Тренд модельдерінің тү рлері
Осы тақ ырыпта тү зу сызық ты тең деу арқ ылы тегістеу тә сілі қ олданылады жә не оны мына формула бойынша есептеуге болады:
Мұ нда
а0 – жә не а1- тү зу сызық тың параметрлері; t - мезгілдік немесе кезең дік уақ ыт мерзімінің рет нө мірі (кү ндер, айлар, жылдар жә не т.б.)
ө сің кілік қ атарлардың уақ ыт кө рсеткіштері t ә рқ ашан белгілі болады. Онда тегістелген қ атардың дә режесін
Мұ нда, y- ө сің кілік қ атардың нақ ты дә режесі; n- қ атардың саны; Бұ ны шешу ү шін
Кесте 5. – Тең демелердің параметрлерін анық тау ү шін жә рднмші қ осымша мә ліметтерді есептеу
Cанды шамалар тең демеде ө з орыгдарына қ ойылғ аннан кейін, жү йе тө мендегі кө ріністе болады:
195=9∙ а0+а1∙ 45 │ х5 1010, 7=а045+а1∙ 285 Белгісіз шаманың бірін жою ү шін (мысалы. а0- ді)бірінші тең демені 5 анына кө бейтіп, кейін бірінші тең демеден екінші тең демені шегеріп тасатймыз:
975=45∙ а0+а1∙ 225 ¯ 1010, 7=а0∙ 45+а1∙ 285
-35, 7=-60∙ а1
Табылғ ан а1=0, 595 шаманы жү йенің бірінші тең дігіне қ ойып, а0 – дің шамасын анық таймыз.
195=9∙ а0+а1∙ 45 195=9∙ а0+0, 595∙ 45 195=9∙ а0+26, 775 9∙ а0=195-26, 775=168, 225
Демек, қ ұ рылғ ан тең деменің у жә не х ортасындағ ы сызық ты байланыс, яғ ни тренд моделі тө мендегі кө ріністе болады.
2005 жыл ү шін нү ктелі болжау: ŷ 1 =18, 6917+0, 595∙ 10 ŷ 2005=18, 6917+5, 95=24, 6417 2006 жыл ү щін нү ктелі болжау: Ŷ 2006=18, 6917+0, 595∙ 11=25, 2367ц/га шитті мақ та ө ндіреді.
2 - мысалда, 1995 - 2004 жж. аралығ ындағ ы он жылдың Оң тү стік Қ азақ стан облыстық статистикалық баскарманың мә ліметтері негізінде кө кө ніс, жеміс, жү зім-шарап кластері бойынша кешеннің техника - экономикалық керсеткіштеріни тренд модельдері мен теориялык дең гейін компьютерде есептеп нә тижесінде 2010 жылғ а даму тенденциясы тө менде анық талды. Кесте 10.5 - Облыс бойынша кө кө ніс, жеміс - жидек жэне жү зімнің ө німділігінің тренд моделдері мен детерминация коэффициентері мә ні.
Табылғ ан а1 параметрінің сандық мә ні ерекше маң ызғ а ие. Мұ нда факторлы белгі х бір бірлікке ө згергенде, у - нә тижелі белгі орташа қ анша бірлікке ө згеруін кө рсетеді. Басқ аша айтканда, ә р гектардан ө ндірілетін ө німнің шығ ымдылығ ы, яғ ни кө кө ніс-1, 1811 центнер, картоп - 11, 669 центнер, жеміс - жидек - 3, 6548 центнер жә не жү зім - 2, 2909 центнер қ арқ ынменен жылдан-жылғ а ө су тенденциясы анық талды. Олардың летерминациялық коэффициентері сә йкесінше 0, 9338; 0, 9620; 0, 6212; 0, 7837-ні қ ұ рады. Егер у нә тижелі кө рсеткіштердің t факторлық белгісі байланысының статистикалық мә ні сызық ты байланыс болса, онда детерминация коэффициенті - 1-ге жақ ын болады, R2 - детерминация коэффициентінің, яғ ни нә тижелі кө рсеткіштен ә сер етуші фактордың арасындағ ы байланыстың тығ ыздық мә нін бағ алау ү шін Ғ - Фишер критериясы (бағ алауы)-ның нө лдік гипотезасы тексеріледі. Бұ л болжамдағ ан гипотеза, қ абылдау немесе қ абылданбаудың дұ рыстығ ын бағ алауғ а жә не шешім қ абылдауғ а мү мкіндік береді.
|














 - тегістелген қ атардың дә режесі;
- тегістелген қ атардың дә режесі;
 ,
,  ,
,  ,
,  шамаларды есептеп шығ у қ ажет. Тренд модельдерінің тү рі мен оның параметрлерін анық тау ү шін қ осымша 5- кесте қ ұ рамыз.
шамаларды есептеп шығ у қ ажет. Тренд модельдерінің тү рі мен оның параметрлерін анық тау ү шін қ осымша 5- кесте қ ұ рамыз.



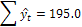


 нә тижесінде а1=0, 595 ц/га
нә тижесінде а1=0, 595 ц/га





