Абсолютні та відносні показники виміру ризику на основі статистичного методу оцінки
1) середнє очікуване значення (математичне очікування); 2) коливання (мінливість) можливого результату. Середнє очікуване значення (
де Середнє очікуване значення вимірює результат, який ми очікуємо в середньому. Середня величина ( Однак для прийняття рішення необхідно так само виміряти коливання показників, тобто визначити міру мінливості можливого результату. Коливання можливого результату являє собою ступінь відхилення очікуваного значення від середньої величини. Для цього на практиці звичайно застосовують два близько пов'язаних критерії: «дисперсію» і «середньоквадратичне відхилення». Дисперсія — середнє зважене з квадратів відхилень дійсних результатів від середніх очікуваних.
Середньоквадратичне відхилення — це корінь квадратний з дисперсії. Він є іменованою величиною і вказується в тих же одиницях, у яких виміряється; ознака, що варіює:
Дисперсія і середньоквадратичне відхилення служать мірами абсолютного коливання і вимірюються в тих же фізичних одиницях, у яких вимірюється ознака, що варіює. Для аналізу звичайно використовується коефіцієнт варіації. Коефіцієнт варіації являє собою відношення середньоквадратичного відхилення до середньої арифметичної і показує ступінь відхилення отриманих знань:
Коефіцієнт варіації — відносна величина. Тому на його розмір не впливають абсолютні значення досліджуваного показника. За допомогою коефіцієнта варіації можна порівнювати навіть коливання ознак, виражених у різних одиницях виміру. Коефіцієнт варіації може змінюватися від 0 до 100%. Чим більший коефіцієнт, тим сильніше коливання. В економічній статистиці встановлена така оцінка різних значень коефіцієнта варіації: До 10% — слабке коливання; До 10-25% — помірне; Понад 25% — високе. Відповідно, чим вище коливання, тим більший ризик. Перевага статистичного методу— простота математичних розрахунків, а явний недолік — необхідність великої кількості вихідних даних, оскільки чим більший масив вихідних даних, тим точніший розрахунок. За допомогою статистичного методу оцінки ризику можна оцінити не тільки ризик конкретної угоди, а й підприємства в цілому за певний проміжок часу. Найбільш поширена точка зору, згідно з якою мірою ризику певного комерційного (фінансового) рішення чи операції слід вважати середньо квадратичне відхилення (позитивний квадратний корінь з дисперсії) значення показника ефективності цього рішення чи операції. Дійсно, оскільки ризик обумовлений недетермінованістю результату рішення (операції), то чим менший розкид (дисперсія) результату рішення, тим більше він передбачуваний, тобто менше ризик. Якщо варіація (дисперсія) результату дорівнює нулю, то ризик повністю відсутній. Наприклад, в умовах стабільної економіки операції з державними цінними паперами вважаються безризиковими. Найчастіше показником ефективності фінансового рішення (операції) служить прибуток. Розглянемо як ілюстрацію вибір певною особою одного з двох варіантів інвестицій в умовах ризику. Припустимо, є два проекти А і В, у які зазначена особа може вкласти кошти. Проект A у визначений момент у майбутньому забезпечує випадкову величину прибутку. Припустимо, що її середнє очікуване значення (математичне очікування), дорівнює а) b) с) d) e) В останніх двох випадках рішення про вибір проекту А чи В залежить від ставлення до ризику особи, що приймає рішення (ОПР). Зокрема, у випадку d проект А забезпечує вищий середній прибуток, однак він і більш ризикований. Вибір при цьому визначається тим, якою додатковою величиною середнього прибутку компенсується для ОПР задане збільшення ризику. У випадку для проекту А ризик менший, але й очікуваний прибуток менший. Однак статистичним методом неможливо користуватися, якщо досліджуваний об'єкт — нове недавно зареєстроване підприємство. Відзначимо, що дисперсія сигналізує про наявність ризику, але при цьому приховує напрямок відхилення від очікуваного значення. Підприємцю часто потрібно, знати, що найбільш імовірно: втрати чи прибуток у результаті здійснення угоди.
|

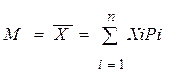 где хі — значение случайной величины, і = 1, 2, … n, рі — соответствующие вероятности.
где хі — значение случайной величины, і = 1, 2, … n, рі — соответствующие вероятности.



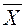 = М) — це середньозважене значення величини події, що зв'язана з невизначеною ситуацією.
= М) — це середньозважене значення величини події, що зв'язана з невизначеною ситуацією. , (10.1)
, (10.1) — значення випадкової величини.
— значення випадкової величини.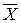 ) являє собою узагальнену кількісну характеристику і не дозволяє прийняти рішення на користь якого-небудь варіанту вкладення капіталу.
) являє собою узагальнену кількісну характеристику і не дозволяє прийняти рішення на користь якого-небудь варіанту вкладення капіталу.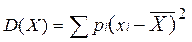 (10.2)
(10.2) чи
чи 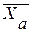 з дисперсією
з дисперсією  . Для проекту В ці числові характеристики прибутку як випадкової величини передбачаються рівними відповідно
. Для проекту В ці числові характеристики прибутку як випадкової величини передбачаються рівними відповідно 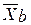 з дисперсією
з дисперсією  . Середньоквадратичні відхилення дорівнюють відповідно
. Середньоквадратичні відхилення дорівнюють відповідно 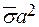 і
і  , слід обрати проект А;
, слід обрати проект А; , слід обрати проект А;
, слід обрати проект А; , слід обрати проект А;
, слід обрати проект А;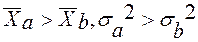 ;
;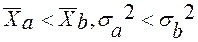 .
.


