Аксиомы статики

Основные понятия статики.

Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.

Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не де­формируются, не изменяют свою форму и объем, какое бы действие на них не было оказано.

Исследованием движения нетвердых тел – упругих, пластичных, жидких, газообразных, занимаются другие науки (сопротивление мате­риалов, теория упругости, гидродинамика и т.д.).

Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам.

Основные понятия:

1. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой.

Сила является величиной векторной.

Ее действие на тело опре­деляется: 1) численной величиной или модулем силы, 2) направле­нием силы, 3) точкой приложения силы (рис.9).

Рис.9

 

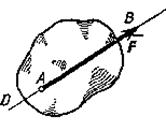
Прямая DE, вдоль которой направлена сила, называется линией действия силы.

В тексте вектор силы обозначается ла­тинскими буквами , , и др., с черточками над ними. Если черточки нет, значит у силы известна только ее чис­ленная величина - модуль.

Рис. 1.2.

Предполагается, что действие силы на тело не изменится, если ее перене­сти по линии действия в любую точку тела (конечно – твердого тела). Поэтому вектор силы называют скользящим вектором. Если силу перенести в точку, не расположенную на этой линии, действие ее на тело будет совсем другим.

2. Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил.

3. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, на­зывается свободным.

4. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состоя­ния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.

5. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или экви­валентной нулю.

6. Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Таким образом, равнодействующая - это сила, которая одна заменяет действие данной системы сил на твердое тело.

7. Сила, равная равнодействующей по модулю, прямо противополож­ная ей по направлению и действующая вдоль той же прямой, назы­вается уравновешивающей силой.

8. Силы, действующие на твердое тело, можно разделить на внешние и внутренние. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга.

9. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Силы, действующие на все точки дан­ного объема или данной части поверхности тела, называются распре­деленными.

Понятие о сосредоточенной силе является условным, так как практически приложить силу к телу в одной точке нельзя. Силы, которые мы в механике рассматриваем как сосредоточенные, пред­ставляют собою по существу равнодействующие некоторых систем распределенных сил.

В частности, обычно рассматриваемая в механике сила тяжести, действующая на данное твердое тело, представляет собою равно­действующую сил тяжести его частиц. Линия действия этой равно­действующей проходит через точку, называемую центром тяжести тела.

Аксиомы статики.

Все теоремы и уравнения статики выво­дятся из нескольких исходных положений, принимаемых без матема­тических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике.

Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F ₁ = F ₂) и направлены вдоль одной прямой в противоположные стороны (рис. 10).

 

Рис.10

 

Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равнове­сии не может.

Аксиома 2. Действие данной си­стемы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.

Эта аксиома устанавливает, что две системы сил, отличающиеся на уравнове­шенную систему, эквивалентны друг другу.

Следствие из 1-й и 2-й аксиом. Действие силы на абсо­лютно твердое тело не изменится, если перенести точку при­ложения силы вдоль ее линии действия в любую другую точку тела.

Рис.11

 

В самом деле, пусть на твердое тело действует приложенная в точке А сила (рис.11). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы и , такие, что = , = . От этого действие силы на тело не изменится. Но силы и со­гласно аксиоме 1 также образуют уравновешенную систему, которая может быть отброшена. В резуль­тате на тело. Будет действовать только одна сила , равная , но приложен­ная в точке В.

Таким образом, вектор, изобра­жающий силу , можно считать приложенным в любой точке на линии действия силы (такой вектор называется скользящим).

Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю па­раллелограмма, построенного на этих силах, как на сторонах.

Вектор , равный диагонали параллелограмма, построенного на векторах и (рис.12), называется геометрической суммой векторов и : = + .

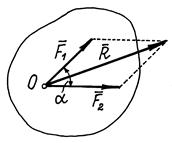
Рис.12

Величина равнодействующей

Рис. 1.3.

Конечно, Такое равен­ство будет соблюдаться только при условии, что эти силы направлены по одной пря­мой в одну сторону. Если же векторы сил окажутся перпендикулярными, то

Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействую­щую, равную геометрической (векторной) сумме этих сил и прило­женную в той же точке.

Аксиома 4. При всяком действии одного материального тела на другое имеет место такое же по величине, но проти­воположное по направлению противодействие.

Закон о равенстве действия и противодей­ствия является одним из основных законов ме­ханики. Из него следует, что если тело А дей­ствует на тело В с силой , то одновременно тело В действует на тело А с такой же по модулю и направленной вдоль той же прямой, но противоположную сторону силой = (рис. 13). Однако силы и не образуют урав­новешенной системы сил, так как они приложены к разным телам.

Рис.13

Аксиома 5 (принцип отвердевания). Равновесие изме­няемого (деформируемого) тела, находящегося под действием дан­ной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым).

Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сва­ренными друг с другом и т. д.
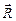