Решение типовых задач. Задача 1. Имеются следующие данные о производстве и себестоимости продукции на двух предприятиях за два квартала:Задача 1. Имеются следующие данные о производстве и себестоимости продукции на двух предприятиях за два квартала:
Определить среднюю себестоимость продукции в каждом квартале. Решение Для того, чтобы выбрать форму расчета средней, необходимо записать логическую формулу осредняемого показателя, в нашем примере – себестоимости:
В первом квартале известна себестоимость (признак х) и объем производства (частота f), то есть дан знаменатель логической формулы, поэтому средняя себестоимость рассчитывается на основе средней арифметической взвешенной:
Во втором квартале по условию отсутствует объем производства, но известен числитель логической формулы (М) - стоимость выпуска продукции. Следовательно, в данном случае необходимо воспользоваться формулой средней гармонической взвешенной:
Таким образом, во втором квартале по двум предприятиям себестоимость увеличилась в среднем на 0, 48 грн., несмотря на то, что на каждом предприятии себестоимость уменьшилась. На такое увеличение повлияли изменения в структуре выпуска продукции предприятиями. Задача 2. Имеются следующие данные об экспорте продукции металлургического комбината:
Определить средний удельный вес продукции на экспорт. Решение Логическая формула осредняемого показателя:
По условию задачи известен числитель – стоимость продукции на экспорт. Поэтому при решении используется формула средней гармонической взвешенной. М – стоимость продукции на экспорт; х – удельный вес продукции на экспорт. Средний удельный вес продукции на экспорт:
Задача 3. Имеются следующие данные о затратах времени на изготовление одной детали рабочими бригады:
Определить средние затраты времени на изготовление одной детали, а также моду и медиану. Решение 1. Средние затраты времени на изготовление одной детали определяем по формуле средней арифметической взвешенной (условные обозначения записаны в таблице):
Для каждого интервала предварительно вычислялось среднее значение признака как полусумма нижнего и верхнего значений интервала. Величина открытых интервалов приравнивается к величине примыкающих к ним соседних интервалов: Таким образом, средние затраты времени на изготовление одной детали составили 29 мин. 2. Для определения моды вначале определяем модальный интервал – т.е. интервал, который встречается чаще всего. Это интервал 28 -30 мин. (у него максимальная частота – 10 чел.). Моду определяем по формуле:
Таким образом, чаще всего затраты времени на одну деталь составляли 29, 3 мин. 3. Для определения медианы составим таблицу, в которой определим накопленную частоту.
Медианным является интервал 28 – 30 мин., так как на этот интервал приходится первая накопленная частота, превысившая половину объема совокупности (20 превышает Медиану определяем по формуле:
Таким образом, половина рабочих затрачивала на изготовление одной детали менее 28, 5 мин, а половина – более 28, 5 мин.
|
.
; 
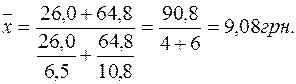
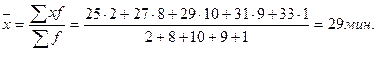
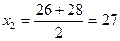и т.д.
).
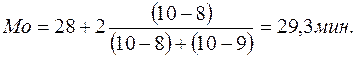
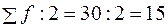