Решение типовых задач. Задача 1. На предприятии в порядке случайной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за октябрь:
Задача 1. На предприятии в порядке случайной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за октябрь:
Определить: 1) среднемесячный размер дохода у работников данного предприятия, гарантируя результат с вероятностью 0, 997; 2) долю рабочих предприятия, имеющих месячный доход 280 грн. и выше, гарантируя результат с вероятностью 0, 954; 3) необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0, 954 предельная ошибка выборки не превышала 10 грн.; 4) необходимую численность выборки при определении доли рабочих с размером месячного дохода 280 грн. и выше, чтобы с вероятностью 0, 954 предельная ошибка не превышала 4%.
Решение
1). Доверительный интервал среднего размера месячного дохода работников предприятия: Средний месячный доход по выборке составит:
Предельная ошибка выборки:
При вероятности Определим дисперсию дохода:
Таким образом, с вероятностью 0, 997 можно утверждать, что месячный доход работников предприятия больше 241, 82 грн. и меньше 276, 58 грн.
2). w – доля рабочих, имеющих размер месячного дохода 280 и выше: w Предельная ошибка доли При вероятности
Доверительные интервалы для генеральной доли:
Доля рабочих предприятия, имеющих доход 280 грн. и выше, находится в пределах от 19, 5 % до 36, 5 %.
3. Необходимая численность выборки для определения среднего месячного дохода определяется по формуле
По условию задачи известны: при вероятности
4. Необходимая численность выборки для определения доли рабочих, имеющих доход 280 грн. и выше, определяется по формуле
По условию задачи известны:
Задача 2. Для определения урожайности зерновых культур проведено выборочное обследование 100 хозяйств региона различных форм собственности, в результате которого получены сводные данные. Необходимо с вероятностью 0, 954 определить предельную ошибку выборочной средней и доверительные пределы средней урожайности зерновых культур по всем хозяйствам региона.
Распределение урожайности по хозяйствам региона, имеющим различную форму собственности
Решение Поскольку обследованные хозяйства региона сгруппированы по формам собственности, предельную ошибку средней урожайности определяем по формуле для типической выборки, осуществляемой методом повторного отбора (численность генеральной совокупности N неизвестна):
В этой формуле неизвестна средняя из внутригрупповых дисперсий. Она исчисляется по формуле:
Для заданной в условии вероятности
Генеральная средняя:
Предельная относительная ошибка выборки, %:
Доверительные пределы генеральной средней исчисляем, исходя из двойного неравенства:
Задача 3. По городской телефонной сети в порядке случайной выборки (механический отбор) произвели 100 наблюдений и установили среднюю продолжительность одного телефонного разговора 5 мин. при среднем квадратическом отклонении 2 мин. Какова вероятность того, что ошибка репрезентативности при определении средней продолжительности телефонного разговора не превысит 18 сек.?
Решение
По условию задачи известны: объем выборки – n =100 выборочная средняя - выборочное среднее квадратическое отклонение – предельная ошибка выборки -
t =
Затем по таблице на основе значения t определяется вероятность того, что ошибка не превысит заданной величины. При t = 1, 5 вероятность P = 0, 866.
Задача 4. На основе выборочного обследования в отделении связи города предполагается определить долю писем частных лиц в общем объеме отправляемой корреспонденции. Никаких предварительных данных об удельном весе этих писем в общей массе отправляемой корреспонденции не имеется. Требуется определить численность выборки, если результаты выборки даны с точностью до 1% и гарантируют это с вероятностью 0, 95.
Решение По условию задачи известны: размер допустимой (предельной) ошибки - принятая вероятность – P = 0, 95; при P = 0, 95 t = 1, 96 (см. приложение 3) Необходимая численность выборки: n = Так как значение w не дано, то следует ориентироваться на наибольшую дисперсию, которой соответствует значение w = 0, 5. n = Таким образом, чтобы с заданной точностью определить долю частных писем в общем объеме отправляемой корреспонденции, необходимо в порядке случайной выборки отобрать 9604 письма.
|

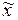 –
– 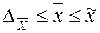 +
+ 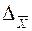 .
. ;
; 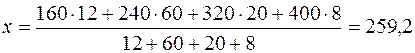 грн.
грн.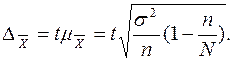

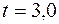 .
.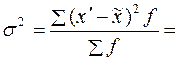
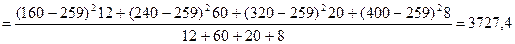
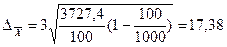 грн.
грн.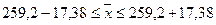 ;
; 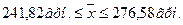
 .
.
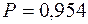
 .
.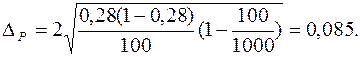


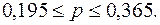
 .
.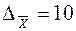 грн.;
грн.; 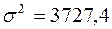 (по данным предыдущей выборки).
(по данным предыдущей выборки). чел.
чел.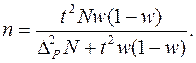
 или 0, 02; при вероятности Р = 0, 954 t = 2; w = 0, 28 (по данным предыдущей выборки).
или 0, 02; при вероятности Р = 0, 954 t = 2; w = 0, 28 (по данным предыдущей выборки).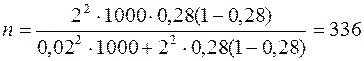 чел.
чел.
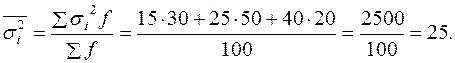
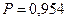
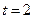 . Тогда предельная ошибка выборки составит, ц/га:
. Тогда предельная ошибка выборки составит, ц/га: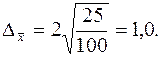
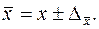 Для нахождения ее границ вначале нужно исчислить среднюю урожайность по выборочной совокупности:
Для нахождения ее границ вначале нужно исчислить среднюю урожайность по выборочной совокупности: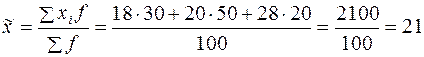 ц/га.
ц/га.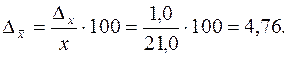
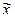 –
– 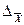 ;
;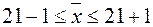 ;
; .
.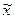 =5 мин.;
=5 мин.; = 2 мин.;
= 2 мин.;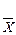 ; µ
; µ  =
= 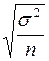 =
= 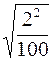 =0, 2 мин.;
=0, 2 мин.; =
= 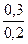 =1, 5.
=1, 5. = 1% или 0, 01;
= 1% или 0, 01;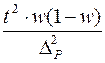
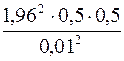 =9604
=9604


