Основные свойства функций
Опр-ть процент выполнения плана по комплектности на предприятии, если известно, что для укомплектования изд. Б необх: 6 шт.-Б1, 6 шт-Б2, 2 шт –Б3, 1 шт-Б4. По плану предусмотрено изготовить 3060 шт. изд. Б в год. Фактически было изготовлено:
Атрощенкова И.Е., Кацуба В.С.
Практикум по высшей математике.
Функции одной переменной. Предел, непрерывность, дифференцируемость.
Оглавление
§1. Функция, основные понятия.
Пусть дано числовое множество Правило, устанавливающее соответствие между
В этой записи Число Если функция Если функция Функции вида Графиком функции К основным элементарным функциям относятся: степенные, показательные, логарифмические, тригонометрические, обратные тригонометрические и гиперболические функции.
Пример 1. Дана функция
Решение. Для нахождения значений функции надо подставить вместо
Данная функция не определена, если знаменатель дроби обращается в ноль, т.е. при
Пример 2. Дана функция Найти
Решение. Функция Так как значение Точка Точки График функции:
Пример 3. Найти область определения функции: a) б) Решение. а) Дробь определена только в том случае, если ее знаменатель не обращается в ноль, т.е. если
б) Так как квадратный арифметический корень определен на множестве неотрицательных чисел, то должны одновременно выполняться неравенства
в) Область определения функции
г) Логарифмическая функция определена на множестве положительных чисел, значит
Пример 4. Найти функции, обратные данным: а) Решение. а) Решая уравнение относительно
б) По смыслу уравнения, которым определяется функция имеем что,
в) Данная функция не задает взаимно однозначного соответствия, т.к. различным значениям x из области определения D(y)=
г) Эта функция на указанной области определения Решим уравнение
но т.к.
Пример 5. Представить сложные функции в виде композиции основных элементарных функций: а) Решение. а) б)
Пример 6. Найти композиции Решение. а) б)
Самостоятельная работа.
Вариант 1. 1. Найти область определения функций: а) б) 2. Представить сложные функции в виде композиции основных элементарных функций: а)
Вариант 2. 1. Найти область определения функций: а) б) 2. Представить сложные функции в виде композиции основных элементарных функций: а)
Вариант 3. 1. Найти область определения функций: а) б) г) 2. Представить сложные функции в виде композиции основных элементарных функций: а)
Ответы. Вариант 1: 1а) Вариант 2: 1а) Вариант 3: 1а) г)
Основные свойства функций. Четность Функцию Если функция не является ни четной, ни нечетной, то ее называют функцией общего вида, или говорят, что функция свойством четности не обладает. График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.
Периодичность Число Функцию, имеющую период называют периодической. Если Т – период функции, то для любого Если функция имеет наименьший положительный период, то он берется в качестве основного. График периодической функции с периодом Т функции при сдвиге вдоль оси абсцисс на Т переходит в себя. Тригонометрические функции
Пример 1. Исследовать функции на четность: а) в) Решение. а) Функция определена при Значит,
б) Функция определена при
в) Хотя формально
Пример 2. Определить, какие из функций являются периодическими, указать их наименьший период: а) г) Решение. а) периодическая,
б) периодическая,
в) непериодическая;
г) периодическая,
д) непериодическая;
е) периодическая,
Самостоятельная работа.
Вариант 1. 1. Исследовать функции на четность: а) в) 2. Найти основной период функции:
Вариант 2. 1. Исследовать функции на четность: а) б) 2. Найти основной период функции:
Вариант 3. 1. Исследовать функции на четность: а) 2. Найти основной период функции:
Ответы. Вариант 1: 1а)четная; б)нечетная; в) общего вида; 2) Вариант 2: 1а)нечетная; б) четная; в) общего вида; 2) Вариант 3: 1а) четная; б)нечетная; в) общего вида; 2)
Дополнительные упражнения. 1. Найти область определения функции: а) б) д) 2. Исследовать функции на четность: а) б) 3. Найти основные периоды функций: а) в)
Ответы.
1.а) г) 2.а) четная; б) общего вида; в) четная; г) четная. 3. а)
|


 , и пусть каждому
, и пусть каждому  поставлено в соответствие единственное число
поставлено в соответствие единственное число  . Тогда говорят, что на множестве
. Тогда говорят, что на множестве  определена числовая функция.
определена числовая функция.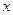 и
и 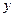 , обозначают некоторым символом, например,
, обозначают некоторым символом, например,  , и пишут
, и пишут
 называют областью определения функции, обозначают
называют областью определения функции, обозначают  .
. , соответствующее значению аргумента
, соответствующее значению аргумента  , называют значением функции при
, называют значением функции при  (значением функции в точке
(значением функции в точке  .Множество значений функции обозначают
.Множество значений функции обозначают  .
. определена на области D, G – ее область значений, функция
определена на области D, G – ее область значений, функция  определена на области G, то функция
определена на области G, то функция  называется сложной функцией, составленной из функций
называется сложной функцией, составленной из функций  , или композицией функций
, или композицией функций  осуществляет взаимно однозначное отображение области D на область E, то можно однозначно выразить
осуществляет взаимно однозначное отображение области D на область E, то можно однозначно выразить 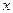 через
через 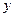 :
:  . Последняя функция называется обратной по отношению к функции
. Последняя функция называется обратной по отношению к функции  , переобозначив ее аргумент через
, переобозначив ее аргумент через 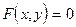 также задает функциональную зависимость между x и y. В этом случае по определению
также задает функциональную зависимость между x и y. В этом случае по определению  . Найти
. Найти  . При каком значении
. При каком значении  и вычислить:
и вычислить: ,
, .
. .
. .
. . Построить график функции.
. Построить график функции.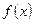 определена на отрезке
определена на отрезке  с помощью трех формул, т.е. является кусочно заданной.
с помощью трех формул, т.е. является кусочно заданной. , то
, то  .
. , поэтому
, поэтому  .
. и
и 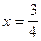
 и, следовательно,
и, следовательно, 

 ;
; ; в)
; в)  ; г)
; г)  .
. . Значит, областью определения функции является множество всех действительных чисел, кроме
. Значит, областью определения функции является множество всех действительных чисел, кроме  . Записывают это так:
. Записывают это так: 

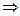
 . Таким образом,
. Таким образом,  .
. задается неравенством
задается неравенством  . Следовательно, нахождение области определения данной функции сводится к решению неравенства
. Следовательно, нахождение области определения данной функции сводится к решению неравенства  . Возводя в квадрат, получим равносильную систему:
. Возводя в квадрат, получим равносильную систему:
 , т.е.
, т.е.  или
или  . Таким образом,
. Таким образом, 
 , б)
, б)  , в)
, в)  , г)
, г)  .
. . Эта функция и будет обратной для данной. Переобозначив x на y и y на x в обратной функции, получим
. Эта функция и будет обратной для данной. Переобозначив x на y и y на x в обратной функции, получим  .
. и
и  . Возводя в квадрат, получим обратную функцию
. Возводя в квадрат, получим обратную функцию  . Переобозначив ее аргумент и функцию, получим
. Переобозначив ее аргумент и функцию, получим  , где
, где  . Значит, для нее нет обратной функции.
. Значит, для нее нет обратной функции. задает взаимно однозначное соответствие, т.е. каждому значению
задает взаимно однозначное соответствие, т.е. каждому значению  относительно
относительно 


 , то получим
, то получим  или, переходя к обычным обозначениям,
или, переходя к обычным обозначениям,  , где
, где  .
. ; б)
; б)  .
. , и тогда
, и тогда 
 , тогда
, тогда 
 и
и  функций, заданных формулами: а)
функций, заданных формулами: а)  ; б)
; б) 


 ;
; ; в)
; в)  ; г)
; г) 
 ; б)
; б)  .
. ;
; в)
в)  г)
г)  .
. ; б)
; б)  .
.
 в)
в)  ;
;
 б)
б)  .
.  б)
б)  в)
в)  г)
г) 
 ; б)
; б)  ; в)
; в)  г)
г)  .
. б)
б)  в)
в) 
 .
. , и называют нечетной, если для любого
, и называют нечетной, если для любого 
 называют периодом функции f(x), если для любого
называют периодом функции f(x), если для любого 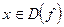 выполнены условия
выполнены условия  и
и  .
.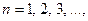 число nT также является периодом этой функции.
число nT также является периодом этой функции. и
и  - периодические с основным периодом T =
- периодические с основным периодом T =  , а
, а  и
и  - с основным периодом T = p.
- с основным периодом T = p. ; б)
; б)  ;
; при
при 
 , т.е. на множестве, симметричном относительно начала координат и
, т.е. на множестве, симметричном относительно начала координат и  .
. , т.е. на промежутке, симметричном относительно 0;
, т.е. на промежутке, симметричном относительно 0; Значит,
Значит,  , но эта функция не обладает свойством четности, т.к. ее область определения
, но эта функция не обладает свойством четности, т.к. ее область определения  несимметрична относительно начала координат.
несимметрична относительно начала координат. , б)
, б)  , в)
, в)  ,
, , д)
, д)  , е)
, е)  .
. , т.к. у функции
, т.к. у функции  , откуда
, откуда  ;
; , т.к. у функции
, т.к. у функции  , то
, то  , откуда
, откуда  ;
; ;
; .
. ; б)
; б)  ;
; .
. .
. ;
; ; в)
; в)  .
.
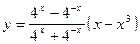 ; б)
; б)  ; в)
; в)  .
. .
. ;
;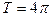 ;
; .
. ;
; ; в)
; в)  ; г)
; г)  ;
; .
. ;
; ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ; в)
; в) 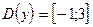 ;
;
 ; д)
; д)  .
. ; в)
; в)  ; г)
; г) 


