Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
.
Число А называется пределом функции  при
при 
(в точке  ), если для любого
), если для любого  , сколь малым бы оно ни было, существует число
, сколь малым бы оно ни было, существует число  , зависящее от
, зависящее от 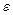 , такое, что при
, такое, что при  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , справедливо неравенство
, справедливо неравенство  .
.
Если А – предел функции 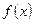 при
при  , то пишут:
, то пишут:
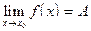 или
или 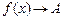 при
при  .
.
В самой точке  функция
функция 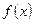 может и не существовать, т.е. значение функции
может и не существовать, т.е. значение функции  может быть не определено.
может быть не определено.
Аналогично запись  означает, что
означает, что
для любого числа  , сколь малым бы оно ни было, существует число
, сколь малым бы оно ни было, существует число  , зависящее от
, зависящее от 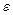 , такое, что при всех
, такое, что при всех  справедливо неравенство
справедливо неравенство  .
.
Говорят, что предел функции 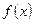 в точке
в точке  равен бесконечности, и пишут
равен бесконечности, и пишут  , если
, если
для любого числа  , сколь большим бы оно ни было, существует число
, сколь большим бы оно ни было, существует число  , зависящее от M, такое, что при всех x, удовлетворяющих неравенству
, зависящее от M, такое, что при всех x, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство 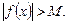
Справедливы следующие основные теоремы о конечных пределах.
Пусть существуют 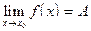 и
и  , тогда
, тогда
1. 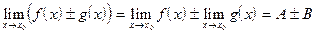
2. 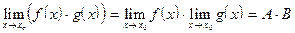
3.  , где
, где 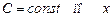
4.  , если
, если 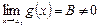
(Все теоремы верны и при  ).
).
Если некоторый предел не может быть вычислен ни по одной из о конечных пределах, ни по теоремам о бесконечно малых и о бесконечно больших функциях, то говорят, что этот предел имеет неопределенность, и указывает ее вид.
Основные виды неопределенностей:
 ,
,  ,
,  .
.
Чтобы вычислить предел, содержащий неопределенность, нужно эту неопределенность раскрыть, то есть преобразовать функцию, стоящую под пределом, так, чтобы неопределенность исчезла.
При вычислении пределов главная задача состоит в том, чтобы научиться раскрывать неопределенности.
Пример 1.
Доказать по определению предела, что  .
.
Решение.
Нам надо доказать, что для любого числа  , сколь малым бы оно ни было, существует такое число
, сколь малым бы оно ни было, существует такое число  , что из неравенства
, что из неравенства  следует неравенство
следует неравенство  .
.
Зададим  и составим неравенство
и составим неравенство

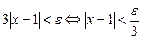 .
.
Тогда если взять  , то для всех значений
, то для всех значений 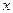 , удовлетворяющих условию
, удовлетворяющих условию  , будет выполняться неравенство
, будет выполняться неравенство  . Следовательно,
. Следовательно,  , что и требовалось доказать.
, что и требовалось доказать.
Пример 2.
Найти 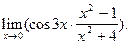
Решение.
Воспользуемся теоремами о конечных пределах и получим, что 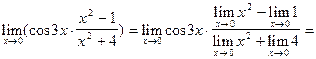
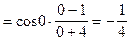 .
.
Правило 1
Eсли предел при  рациональной дроби имеет неопределенность
рациональной дроби имеет неопределенность  , то нужно числитель и знаменатель дроби разложить на множители так, чтобы выделить множитель
, то нужно числитель и знаменатель дроби разложить на множители так, чтобы выделить множитель  , который стремится к нулю при
, который стремится к нулю при  , и сократить на него.
, и сократить на него.
Пример 3.
Найти  .
.
Решение.
Т.к. пределы числителя и знаменателя равны 0, применить теорему о пределе частного нельзя, имеем неопределенность вида  . Разложим числитель и знаменатель на множители и сократим на общий множитель
. Разложим числитель и знаменатель на множители и сократим на общий множитель  , который обращает в нуль числитель и знаменатель. Получим
, который обращает в нуль числитель и знаменатель. Получим

 .
.
Пример 4.
Найти 
Решение.

 .
.
Пример 5.
Найти 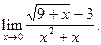
Решение.
Имеем неопределенность вида  . Умножим числитель и знаменатель на выражение, сопряженное числителю
. Умножим числитель и знаменатель на выражение, сопряженное числителю 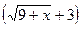 , чтобы, получив разность квадратов в числителе и разложив на множители знаменатель, сократить на
, чтобы, получив разность квадратов в числителе и разложив на множители знаменатель, сократить на 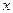 :
:

 .
.
Пример 6.
Найти  .
.
Решение.
Имеем неопределенность вида  . Умножим числитель и знаменатель на неполный квадрат суммы выражения (
. Умножим числитель и знаменатель на неполный квадрат суммы выражения ( ), чтобы получить в знаменателе разность кубов. Далее выделим в числителе и знаменателе множитель
), чтобы получить в знаменателе разность кубов. Далее выделим в числителе и знаменателе множитель  и сократим на него:
и сократим на него:


Правило 2
Чтобы раскрыть неопределенность вида  , образованную при
, образованную при  делением многочленов или иррациональных выражений, нужно вынести за скобки в числителе и знаменателе старшие степени переменной x и сократить дробь под знаком предела.
делением многочленов или иррациональных выражений, нужно вынести за скобки в числителе и знаменателе старшие степени переменной x и сократить дробь под знаком предела.
Пример 7.
Найти  .
.
Решение.
Т.к. числитель и знаменатель дроби неограниченно растут при  , то имеем неопределенность
, то имеем неопределенность  .Для ее раскрытия вынесем за скобки в числителе и знаменателе старшую степень переменной
.Для ее раскрытия вынесем за скобки в числителе и знаменателе старшую степень переменной  и сократим на нее:
и сократим на нее:
 .
.
Здесь учтено, что  и
и  при
при  .
.
Пример 8.
Найти  .
.
Решение.
Аналогично рассмотренному в предыдущем примере: 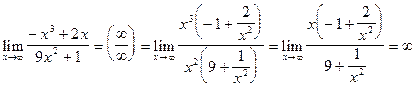
Пример 9.
Найти  .
.
Решение.
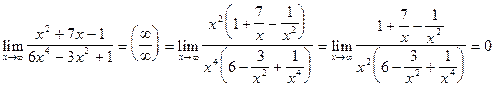
Пример 10. Обобщение результатов предыдущих примеров.
Найти  , где n и m – натуральные числа,
, где n и m – натуральные числа,  .
.
Решение.
Имеем неопределенность  . Вынесем за скобки в числителе
. Вынесем за скобки в числителе  , в знаменателе
, в знаменателе  и получим:
и получим:
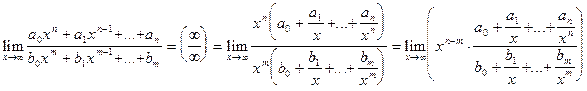
Предел второго множителя равен  . Предел первого множителя зависит от соотношения между числами
. Предел первого множителя зависит от соотношения между числами 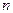 и
и  :
:
если  , то
, то  и, следовательно, общий предел бесконечен;
и, следовательно, общий предел бесконечен;
если  , то
, то  и общий предел
и общий предел 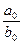 ;
;
если  , то
, то  и общий предел равен нулю.
и общий предел равен нулю.
Итак, получен результат, которым можно пользоваться для раскрытия неопределенностей  , образованных при
, образованных при  делением целых многочленов:
делением целых многочленов:

 .
.
Например,
 так как n = m = 3;
так как n = m = 3;
 так как n =5, m = 4, то есть n > m;
так как n =5, m = 4, то есть n > m;
 так как n =5, m = 6, то есть n < m.
так как n =5, m = 6, то есть n < m.
Правило 3.
Случай, когда при  или
или 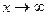 функция
функция 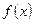 представляет разность двух положительных бесконечно больших величин, т.е. неопределенность
представляет разность двух положительных бесконечно больших величин, т.е. неопределенность  , можно привести к неопределенности
, можно привести к неопределенности  или
или  путем преобразования функции к дроби.
путем преобразования функции к дроби.
Пример 11.
Найти  .
.
Решение.
Так как знаменатель каждой дроби есть величина бесконечно малая при  , а числители есть числа, не равные нулю, то каждая из дробей является бесконечно большой величиной, т.е. имеем неопределенность
, а числители есть числа, не равные нулю, то каждая из дробей является бесконечно большой величиной, т.е. имеем неопределенность  . Чтобы раскрыть ее, приведем дроби к общему знаменателю:
. Чтобы раскрыть ее, приведем дроби к общему знаменателю:
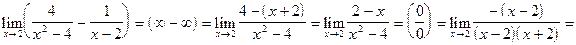
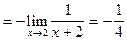 .
.
Пример 12.
Найти  .
.
Решение.
Имеем неопределенность  . Чтобы раскрыть ее, умножим и разделим выражение на
. Чтобы раскрыть ее, умножим и разделим выражение на  . В результате получим:
. В результате получим:

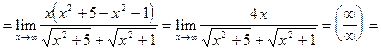

 .
.
Т.к.  , то дальнейшее решение надо проводить отдельно для
, то дальнейшее решение надо проводить отдельно для  и
и  :
:
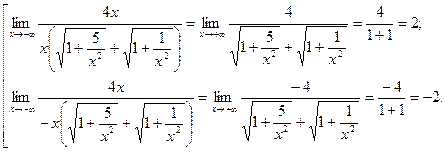
Пример 13.
Найти 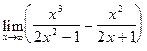 .
.
Решение.
При 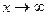 степень числителя больше степени знаменателя у обеих дробей /смотри пример 10 /, значит имеем неопределенность
степень числителя больше степени знаменателя у обеих дробей /смотри пример 10 /, значит имеем неопределенность  . Чтобы раскрыть ее, приведем дроби к общему знаменателю:
. Чтобы раскрыть ее, приведем дроби к общему знаменателю:

(т.к. степени числителя и знаменателя равны, то предел равен отношению коэффициентов при старших степенях).
Самостоятельная работа.
Вариант 1.
Найти: а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Вариант 2.
Найти: а) 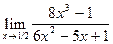 ; б)
; б)  ;
;
в)  ; г)
; г) 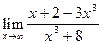 .
.
Вариант 3.
Найти: а)  ; б)
; б)  ;
;
в) 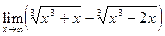 ; г)
; г) 
Ответы.
Вариант 1: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Вариант 2: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Вариант 3: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Дополнительные упражнения.
1. а)б)в)  2.а)б)в)
2.а)б)в) 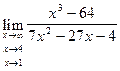
3.  4.
4. 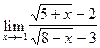
5. 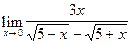 6.
6. 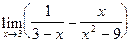
7.  8.
8. 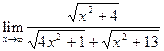
Ответы:
1. а)  , б) , б)  , в) , в)  ; ;
| 5.  ; ;
|
2. а)  , б) , б)  , в) , в) 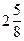 ; ;
| 6.  ; ;
|
| 3. 7;
| 7.  ; ;
|
4.  ; ;
| 8.  . .
|

 определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
.
 ), если для любого
), если для любого  , сколь малым бы оно ни было, существует число
, сколь малым бы оно ни было, существует число  , зависящее от
, зависящее от 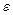 , такое, что при
, такое, что при  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , справедливо неравенство
, справедливо неравенство  .
.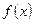 при
при 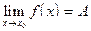 или
или 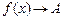 при
при  .
. может быть не определено.
может быть не определено. означает, что
означает, что , зависящее от
, зависящее от  справедливо неравенство
справедливо неравенство  , если
, если , сколь большим бы оно ни было, существует число
, сколь большим бы оно ни было, существует число 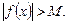
 , тогда
, тогда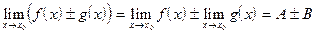
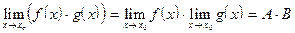
 , где
, где 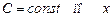
 , если
, если 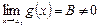
 ).
). ,
,  ,
,  .
. .
. следует неравенство
следует неравенство  .
.
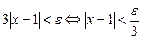 .
. , то для всех значений
, то для всех значений 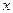 , удовлетворяющих условию
, удовлетворяющих условию  . Следовательно,
. Следовательно, 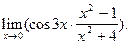
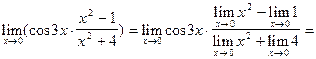
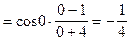 .
. , то нужно числитель и знаменатель дроби разложить на множители так, чтобы выделить множитель
, то нужно числитель и знаменатель дроби разложить на множители так, чтобы выделить множитель  , который стремится к нулю при
, который стремится к нулю при  .
. , который обращает в нуль числитель и знаменатель. Получим
, который обращает в нуль числитель и знаменатель. Получим
 .
.

 .
.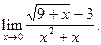
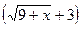 , чтобы, получив разность квадратов в числителе и разложив на множители знаменатель, сократить на
, чтобы, получив разность квадратов в числителе и разложив на множители знаменатель, сократить на 
 .
. .
. ), чтобы получить в знаменателе разность кубов. Далее выделим в числителе и знаменателе множитель
), чтобы получить в знаменателе разность кубов. Далее выделим в числителе и знаменателе множитель  и сократим на него:
и сократим на него:

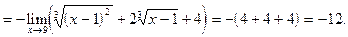
 , образованную при
, образованную при  .
.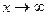 , то имеем неопределенность
, то имеем неопределенность  .
. и
и  при
при  .
.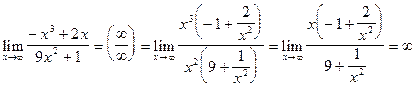
 .
.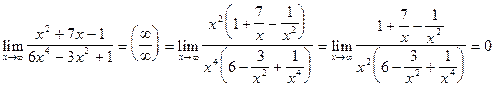
 , где n и m – натуральные числа,
, где n и m – натуральные числа,  .
. , в знаменателе
, в знаменателе  и получим:
и получим: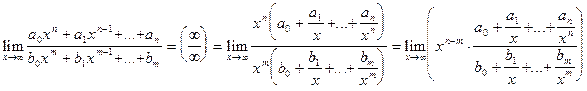
 . Предел первого множителя зависит от соотношения между числами
. Предел первого множителя зависит от соотношения между числами  и
и  :
: , то
, то  и, следовательно, общий предел бесконечен;
и, следовательно, общий предел бесконечен; , то
, то  и общий предел
и общий предел 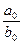 ;
; , то
, то  и общий предел равен нулю.
и общий предел равен нулю. .
. так как n = m = 3;
так как n = m = 3; так как n =5, m = 4, то есть n > m;
так как n =5, m = 4, то есть n > m; так как n =5, m = 6, то есть n < m.
так как n =5, m = 6, то есть n < m. , можно привести к неопределенности
, можно привести к неопределенности  .
. , а числители есть числа, не равные нулю, то каждая из дробей является бесконечно большой величиной, т.е. имеем неопределенность
, а числители есть числа, не равные нулю, то каждая из дробей является бесконечно большой величиной, т.е. имеем неопределенность 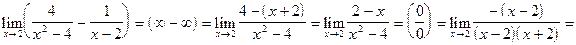
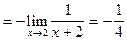 .
. .
. . В результате получим:
. В результате получим:
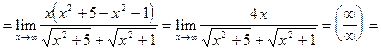

 .
. , то дальнейшее решение надо проводить отдельно для
, то дальнейшее решение надо проводить отдельно для  и
и  :
: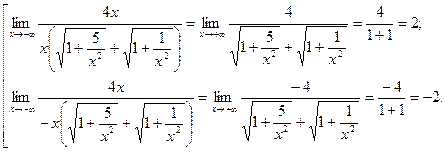
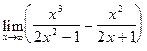 .
.
 ; б)
; б)  ;
; ; г)
; г)  .
.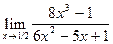 ; б)
; б)  ;
; ; г)
; г) 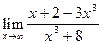 .
. ; б)
; б)  ;
;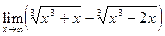 ; г)
; г) 
 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. 2.а)б)в)
2.а)б)в) 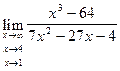
 4.
4. 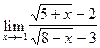
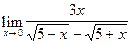 6.
6. 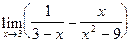
 8.
8. 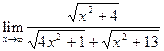
 ;
;
 ;
;
 , в)
, в) 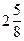 ;
;
 ;
;
 ;
;
 .
.



