Метод Зейделя
Метод Зейделя является модификацией метода итерации. Он заключается в том, что при вычислении (k+1)-го приближения неизвестного Пусть дана приведенная линейная система Выберем произвольно начальные приближения корней Далее, предполагая, что k-е приближения
Процесс повторяется до тех пор, пока разница между двумя соседними приближениями не будет меньше необходимой точности. Условия сходимости те же, что и для метода итераций.
Пример 3.2. Пусть дана линейная система и приближенные корни системы:
Приведем систему к виду, удобному для итераций
Взяв в качестве начальных приближений: при k=1 при k = 2 Найдем разность по модулю между соседними приближениями: | | | Так как для приведенной системы выполняется условие сходимости при Таким образом, в качестве решения можем принять
|
при i> 1 используют уже вычисленные ранее (k+1)-е приближения неизвестных 
,
корней известны, согласно Зейделю будем строить (k+1)-е приближения корней по следующим формулам:
и 
.
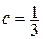поэтому метод сходится
, получим:
- 
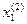| = 0, 00048
- 
| = 0, 00047
- 
| = 0, 00016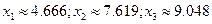
.
